1.Encontrar, se existirem, os pontos de máximos e de mínimos globais das funções:

d)

Como as derivadas parciais em relação a x e y não existem no ponto (0,0), sabemos que se trata, portanto, de um ponto crítico.

Agora, só precisamos determinar se estamos tratando de um ponto de máximo ou mínimo local.

Agora, presta atenção nessas derivadas parciais. Olha essas raízes aí no denominador!!!!! A gente teria que usar a regra do quociente, juntamente com a regra da cadeia, para calcular cada uma das quatro derivadas parciais de segunda ordem. Eu me tremo só de pensar. Você também deveria. Mas calma. Vem comigo que eu tenho uma solução muito mais simples.

Perceba que o gráfico da função coincide com a superfície cônica, com .

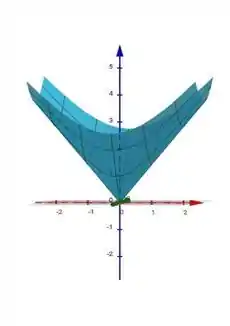
Olha para a figura. Perceba que o gráfico atinge o seu menor valor quando (x,y)=(0,0). Ou seja, (0,0) é o ponto de mínimo global. Além disso, não existem máximos globais, pois o cone “cresce” infinitamente para cima.