22-Esboce um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostra as assíntotas horizontais, verticais, oblíquas e curvilíneas e dê suas equações. Identifique (se houver) os pontos em que o gráfico cruza uma assíntota. Confira seu trabalho com um recurso gráfico.
22-
Passo 1
Galera, a nossa função pode ser escrita assim também:
Bora derivar essa função:
Agora, vamos derivar novamente:
Passo 2
Igualando a primeira derivada a zero, temos:
De cara nós já vemos que é uma das raízes dessa equação, né ?
Agora, nós temos que usar Briott Ruffini para vermos se tem outra raiz:

Como o nosso Briott Ruffini não deu em nada, concluímos que só temos uma raiz: .
Para :
é o nosso ponto estacionário.
O próximo passo é saber se , ou . Isso que vai determinar qual tipo de extremos relativo nós encontramos.
Passo 3
Para :
Como , para , temos um ponto de máximo.
Vamos ver se temos algum ponto de inflexão... Para isso nós temos que fazer um estudo de sinais com a função . Então vamos lá!
Agora, temos que ver como essa função se comporta ao redor desses pontos e, a melhor forma de fazer isso é montando um quadro de sinais.
![]()
Galerissss, como a função varia o sinal, para ., temos um ponto de inflexão.
Para :
é o nosso ponto de inflexão.
Passo 4
Por último, temos que ver as assíntotas.
- Assíntota horizontal:
Dessa forma, não temos assíntota horizontal.
-Assíntota vertical:
Dessa forma, para temos uma assíntota vertical.
-Assíntota oblíqua e curvilínea:
Gente, nós temos a seguinte função:
Podemos reescrever a nossa função assim:
Como a segunda parcela tende a quando , segue que
quando
Assim, temos que é uma assíntota oblíqua, pois o grau do numerador é maior em um do que o grau do denominador.
Por fim, temos o seguinte gráfico:
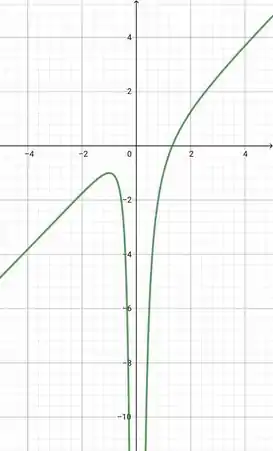
Resposta
(máximo relativo) é o nosso ponto estacionário.
é o nosso ponto de inflexão.
Para temos uma assíntota vertical.
Para temos uma assíntota oblíqua.