Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 33

33. Determine o centroide de uma placa fina e plana que abrange a região compreendida pelas parábolas y = 2 x 2 e y = 3 - x 2 .

Passo 1

Desenhando essas parábolas, vamos ver que essa área vai ficar dessa forma:

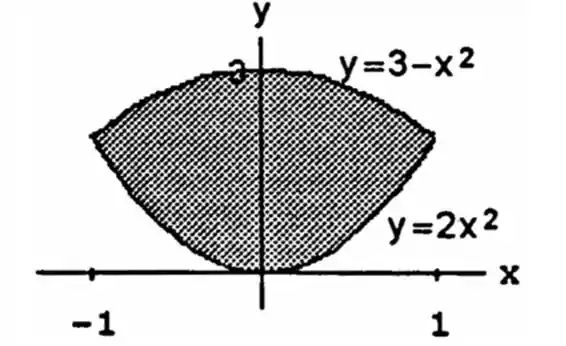
Como não foi falado nada da densidade, vamos considerar ela constante, sendo assim o centroide é igual ao centro de massa:

Pela simetria podemos observar que x - = 0

Para calcular o centro de massa em y , vamos usar as faixas de massa que tem o centro de massa em

x ~ , y ~ = x , y 1 x + y 2 x 2

x ~ , y ~ = x , 2 x 2 + 3 - x 2 2

x ~ , y ~ = x , x 2 + 3 2

O tamanho dessas faixas vão ser:

3 - x 2 - 2 x 2 = 3 1 - x 2

Se multplicarmos o comprimento das faixas por um d x , vamos obter o elemento de área dessas faixas:

d A = 3 1 - x 2 d x

Multiiplicando pela densidade, temos o elemento infinitesimal de massa:

d m = δ ⋅ d A

d m = δ ⋅ 3 1 - x 2 d x

Passo 2

Agora de que temos y ~ e d m podemos calcular o momento em x , M x :

M x = ∫ y ~ d m

Podemos ver no gráfico que os gráficos se interceptam em x = - 1   e x = 1 , ou seja, esses são os limites de integração:

M x = ∫ - 1 1 x 2 + 3 2 ⋅ δ ⋅ 3 1 - x 2 d x

M x = 3 δ 2 ∫ - 1 1 x 2 + 3 ⋅ 1 - x 2 d x

M x = 3 δ 2 ∫ - 1 1 - x 4 - 2 x 2 + 3 d x

M x = 3 δ 2 - x 5 5 - 2 x 3 3 + 3 x - 1 1

M x = 3 δ 2 - 1 5 5 - 2 1 3 3 + 3 1 - 3 δ 2 - - 1 5 5 - 2 - 1 3 3 + 3 - 1

M x = 3 δ 2 - 1 5 - 2 3 + 3 - 1 5 - 2 3 + 3

M x = 3 δ - 1 5 - 2 3 + 3

M x = 3 δ - 3 - 10 + 45 15

M x = 32 δ 5

Passo 3

Para conseguirmos calcular o centro de massa só nos resta saber

M = ∫ d m

M = ∫ - 1 1 δ ⋅ 3 1 - x 2 d x

M = 3 δ ∫ - 1 1 1 - x 2 d x

M = 3 δ x - x 3 3 - 1 1

M = 3 δ 1 - 1 3 - 3 δ - 1 + 1 3

M = 3 δ 1 - 1 3 + 1 - 1 3

M = 3 δ 4 3

M = 4 δ

Passo 4

Agora temos tudo o que precisamos para calcular o centro de massa em y :

y - = M x M

y - = 32 δ 5 4 δ

y - = 32 δ 5 4 δ

y - = 8 5

Resposta

( x - , y - ) = 0 , 8 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área da região limitada pela curva dada(coordenadas polares). c ) ρ = cos ⁡ 2 θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares c )ρ = 1 eρ = 2 1 - cos ⁡ θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares c )ρ = 3 eρ = 2 1 - cos ⁡ θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares e )ρ = cos ⁡ θeρ = sin ⁡ θ
Calcule a área da intersecção da região limitada pelas curvas dadas em coordenadas polares a )ρ = 2 - cos ⁡ θeρ = 1 + cos ⁡ θ