Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.2 - Ex. 35
35. Um quadro com 40cm de altura está colocado numa parede, sendo que sua base está a 30cm acima do nível dos olhos de um observador. Se o observador está se aproximando da parede com uma velocidade de 40 cm/s com que velocidade a medida do ângulo de visão da pintura estará variando quando o observador estiver a 1m da parede?
Passo 1
O que o enunciado nos pede, é para encontrarmos qual é taxa de variação do ângulo de observação quando o observador se encontra a uma dada distância da parede. Para isso, podemos utilizar da mesma linha de raciocínio das questões anteriores parando na derivada de com relação a x.
Passo 2
Um esboço do que está sendo dito no enunciado pode ser representado pela seguinte figura:
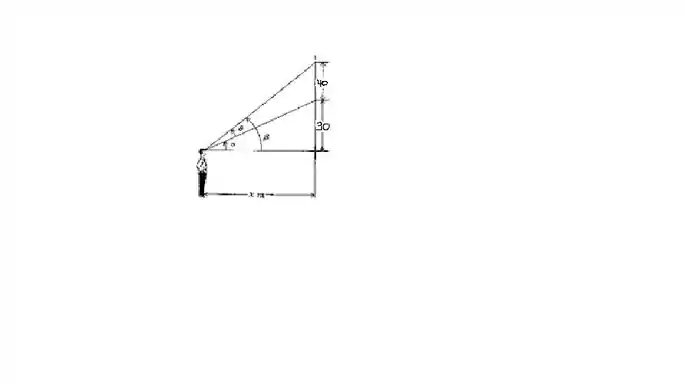
Seja a distância do observador até a parede. Vemos da figura que , vemos também que:
Substituindo esses valores de na relação obtemos :
Sabendo que a distância em questão, é dada por , temos:
Passo 3
Derivando com relação a a função que descreve o comportamento do ângulo em função da distância, teremos:
Assim, quando , temos que:
Logo, a velocidade na qual a medida do ângulo de visão varia é de 1,45.
Resposta
1,45