Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 44

44. A base de um sólido é a região encerrada por um círculo com raio de 4 cm de raio, e cada seção plana perpendicular a um diâmetro fixo da base é um triângulo isósceles com 10 cm de altura e uma corda do cìrculo como base. Ache o volume do sólido.

Passo 1

A questão fala que a base da figura é um circulo e em cima da base tem vários triângulos equiláteros,se liga na imagem:

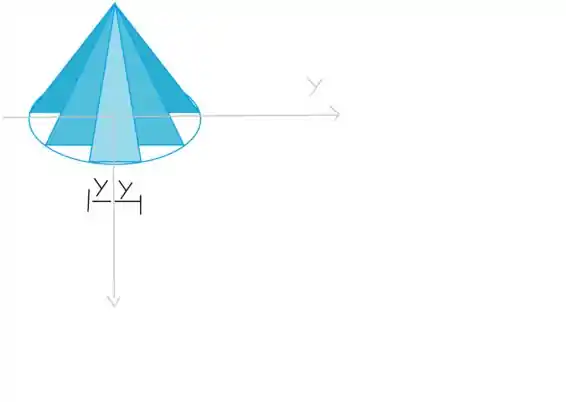
Para montarmos a integral precisamos da área desse triangulo equilátero, a qual será dada por

Passo 2

Iremos reescrever y em função de x, para isso usaremos Pitágoras:

Então, poderá ser reescrito como

Passo 3

A integral ficará assim:

Mas é nesse momento que você se pergunta como resolver essa integral aí, mas calma aí, que tem uma forma bem malandra para fazer.

Passo 4

A função que está dentro da integral é

Ou

Aaaah, essa equação é bem conhecida, é a da circunferência. Portanto, o valor da integral é igual a área de um semi-circulo multiplicado por 10.

Isto é,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sec ⁡ x , y = cos ⁡ x , 0 ≤ x ≤ π 3 , e mt o r n od ey = - 1

Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sin 2 ⁡ ( x ) , y = 0 , 0 ≤ x ≤ π , e mt o r n od ee i x ox

Encontre o volume obtido pela rotação da região delimitada pelas curvas dadas em torno dos eixos especificados y = sin ⁡ x , y = 0 , π 2 ≤ x ≤ π , e mt o r n od oe i x ox

Encontre o volume comum de duas esferas, cada qual com raio r , se o centro de cada esfera está na superfície da outra esfera.

Suponha que a região R tenha área A e esteja acima do eixo x . Quando R é girada em torno de eixo x , ela gera um sólido com volume V 1 . Quando R é girada em torno da reta y = - k (onde k é um número