Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.7 - Ex. 23
Ache as assíntotas horizontal e vertical do gráfico de , determinando o seguinte:
Os extremos relativos de ;
Os pontos de inflexão do gráfico de ;
Os intervalos em que é crescente
Os intervalos em que é decrescente;
Onde o gráfico é côncavo para cima;
Onde o gráfico é côncavo para baixo;
A inclinação de qualquer tangente de inflexão;
As assíntotas horizontal, vertical e oblíqua, se existirem
Passo 1
Vamos começar olharando as assíntotas:
Vamos começar pela assíntota horizontal.
Assíntota horizontal: fazer o limite no infinito. Ou seja,
Vamos calcular esses limites. Primeiro:
Como é temos que pegar a expressão para valores maiores que
Vai ficar:
Então não temos assíntota horizontal desse lado.
Passo 2
O outro vai ser:
Agora pegando a outroa expressão
Vai ficar:
Então não temos assíntota horizontal desse lado.
Passo 3
Agora vamos para as assíntotas oblíquas. Só vamos fazer essas assíntotas se não existirem as horizontais. Elas substituem as horizontais por cada lado.
Se as assíntotas horizontais não existirem, talvez existir a oblíqua. Para isso, devemos achar os coeficientes e de que é a equação da assíntota obliqua.
Para isso, devemos fazer
Se esse valor existir, aí fazemos
Mesma coisa para o
Se esse valor existir, aí fazemos
Passo 4
Aqui, como temos polinômios dos dois lados, podemos achar a derivada só derivando cada expressão.
Vamos achar o limite para ver se existe . Primeiro para
Opa, não apareceu desse lado. Temos que olhar do outro agora
Também não tem, então essa função não tem assíntotas oblíquas.
Passo 5
Vamos para as verticais. Para isso, temos que procurar algum valor de que faça o limite ir para . Normalmente procuramos quando o denominador da fração for . Mas no caso dos polinômios isso não vai existir.
Então quando estivermos trabalhando com polinômios não vamos ter assíntotas verticais.
Passo 6
Vamos aos extremos e os intervalos de crescimento e decrescimento. Para isso temos que analisar o sinal de .
Rpeare que nos dois intervalos a derivada temos , que vai depender do sinal de , sendo negativo com e positivo com .
Quando é negativo ele multiplica o enquanto quando é positivo ele multiplica o . Isso vai fazer a derivada ser sempre positiva.
Então:
A função é crescente se e decrescente se , então:
Passo 7
Agora vamos ver os extremos. Pelo teste da primeira derivada, teremos máximo quando a função vai de crescente para decrescente, e mínimo quando a função for de decrescente para crescente.
Como a derivada tem um sinal só não vamos ter extremos relativos.
Passo 8
Vamos agora para a concavidade e os pontos de inflexão. A função é côncava para cima se e côncava para baixo se .
O ponto vai ser de inflexão quando muda a concavidade.
De novo, para derivada basta derivarmos a expressão direto de novo.
Aquele é sempre positivo, mas quando temos o multiplicando e quando temos o multiplicando. Dessa forma
Concluindo:
Como ela muda a concavidade em , ele é um ponto de inflexão
Passo 9
Para terminar vamos ao esboço. Para isso, precisamos juntar todas as informações.
- Não possui assíntotas;
- ponto de inflexão
- Tangente de inflexão:
- Não possui assíntotas;
- ponto de inflexão
- Tangente de inflexão:
Falta acharmos a tangente de inflexão, que é o valor da derivada no ponto de inflexão
Vamos para o gráfico, ele vai ficar assim:
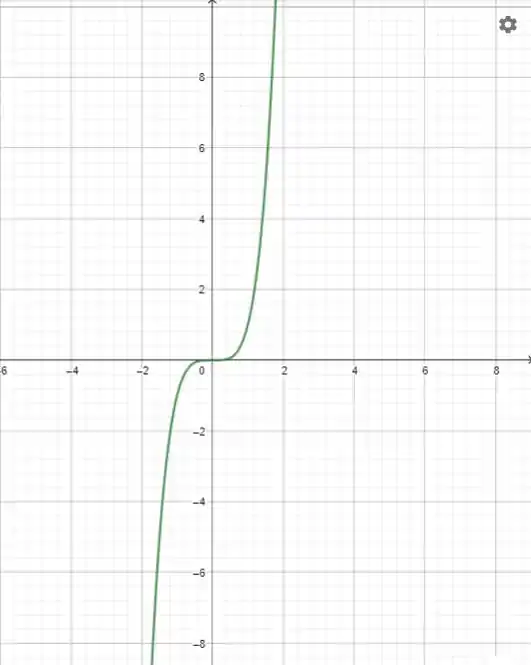
Resposta
Vamos para o gráfico, ele vai ficar assim:
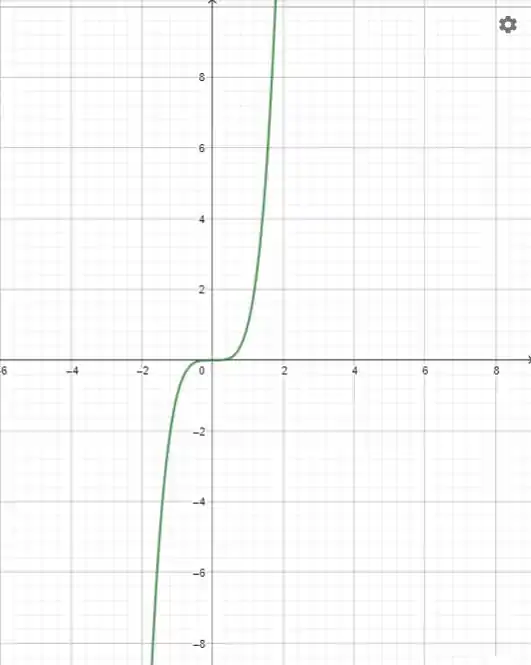
Resposta
Ei, a resposta está no passo a passo :)