Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.7 - Ex. 51
Ache as assíntotas horizontal e vertical do gráfico de , determinando o seguinte:
Os extremos relativos de ;
Os pontos de inflexão do gráfico de ;
Os intervalos em que é crescente
Os intervalos em que é decrescente;
Onde o gráfico é côncavo para cima;
Onde o gráfico é côncavo para baixo;
A inclinação de qualquer tangente de inflexão;
As assíntotas horizontal, vertical e oblíqua, se existirem
Passo 1
Vamos para as assíntotas:
Vamos começar pela assíntota horizontal.
Assíntota horizontal: fazer o limite no infinito. Ou seja,
Passo 2
Agora vamos aos limites. Primeiro:
Vai ficar:
Então não temos assíntota horizontal desse lado.
Passo 3
O outro vai ser:
Vai ficar:
Então não temos assíntota horizontal desse lado.
Passo 4
Agora vamos para as assíntotas oblíquas. Só vamos fazer essas assíntotas se não existirem as horizontais. Elas substituem as horizontais por cada lado.
Se as assíntotas horizontais não existirem, talvez existir a oblíqua. Para isso, devemos achar os coeficientes e de que é a equação da assíntota obliqua.
Para isso, devemos fazer
Se esse valor existir, aí fazemos
Mesma coisa para o
Se esse valor existir, aí fazemos
Passo 5
Para acharmos a derivada, vamos usar a regra do quociente:
Agora vamos aos limites. Primeiro:
Vai ficar:
Também não teremos a oblíquoa.
Passo 6
O outro vai ser:
Vai ficar:
Também não teremos a oblíquoa.
Passo 7
Vamos para as verticais. Para isso, temos que procurar algum valor de que faça o limite ir para . Normalmente procuramos quando o denominador da fração for . Aqui, temos uma potencia racional, que é uma fração na potência. Nesses casos não teremos assíntotas verticais.
Passo 8
Vamos aos extremos e os intervalos de crescimento e decrescimento. Para isso temos que analisar o sinal de .
Vamos ter um expoente na raiz, isso quer dizer que ele vai ser sempre positivo.
Assim, nossa fração vai ser sempre positiva também.
A função é crescente se e decrescente se , então:
Passo 9
Agora vamos ver os extremos. Pelo teste da primeira derivada, teremos máximo quando a função vai de crescente para decrescente, e mínimo quando a função for de decrescente para crescente.
Ela vai ser sempre crescente. Então não tem ponto de extremo .
Passo 10
Vamos agora para a concavidade e os pontos de inflexão. A função é côncava para cima se e côncava para baixo se .
O ponto vai ser de inflexão quando muda a concavidade.
O sinal depende só de , porque o expoente é ímpar. Então:
Assim
Então:
Isso também nos diz que é ponto de inflexão, porque a derivada muda naquele ponto.
Passo 11
Para terminar vamos ao esboço. Para isso, precisamos juntar todas as informações.
- Não possui assíntotas
- ponto de inflexão.
- Tangente de inflexão:
- Não possui assíntotas
- ponto de inflexão.
- Tangente de inflexão:
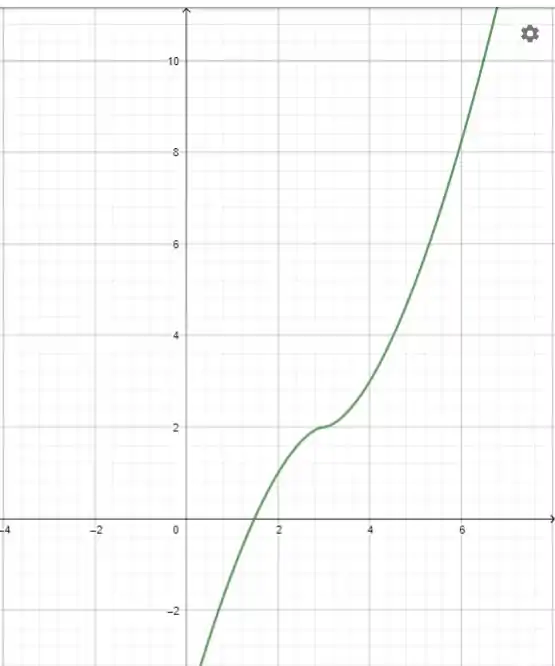
Resposta
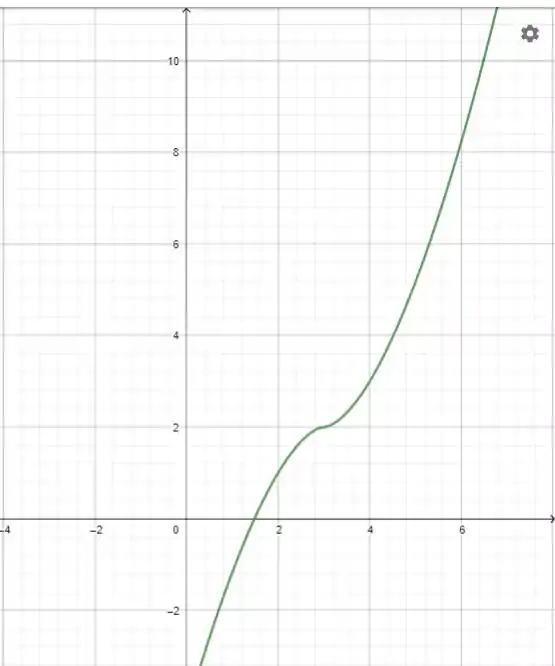
Resposta
Ei, a resposta está no passo a passo :)