Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 3
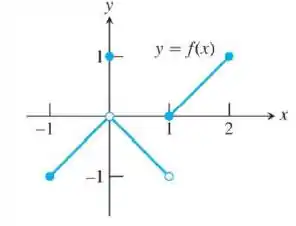
Quais das afirmações a seguir com relação à função representada graficamente aqui são verdadeiras? E quais são falsas?
existe
existe em todo em
não existe
Passo 1
Questão envolvendo limite num ponto e gráfico só tem uma coisa a se fazer: olhar o gráfico da função um pouco a esquerda (vamos chamar isso de ) e um pouco a direita (vamos chamar isso de ) de .
Se os gráficos coincidirem, ótimo o limite existe e vale o valor do gráfico naquele ponto! Se não coincidir o limite não vai existir!
Essa questão envolve 2 pontos () e depois um intervalo . Então vamos calcular esses limites separadamente e depois analisamos as afirmações que ele deu!
Passo 2
Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:
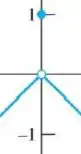
Olhando pela esquerda, vemos que a função se aproxima de 0, ou seja:
Olhando pela direita, vemos que a função se aproxima de 0, ou seja:
Como os limites deram iguais, temos que:
OBS: Só olhamos os valores da função ao redor do ponto e não exatamente o valor da função no ponto, ok?! Mesmo , ao redor do ponto a função está indo para que é o valor do limite.
Passo 3
b) Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:
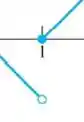
Olhando pela esquerda, vemos que a função se aproxima de -1, ou seja:
Olhando pela direita, vemos que a função se aproxima de 0, ou seja:
Tá vendo como deu diferente? Então o limite não existe!
Passo 4
Vamos olhar agora para o intervalo como um todo. Desenhei ele aqui embaixo para ficar mais fácil:
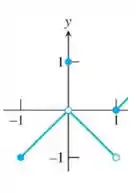
Para todos os pontos entre e , vemos que a função se aproxima da mesma forma tanto pela direita quanto pela esquerda, então o limite existe! Só para não restar dúvidas, dá um check no desenho que eu fiz aqui embaixo para um ponto qualquer do intervalo:
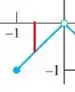
No ponto , nós já analisamos e vimos que o limite existe e vale .
Para todos os pontos entre e , temos a mesma situação do início do passo, ou seja, a função se aproxima dos mesmos valores tanto pela esquerda quanto pela direita, então o limite existe em todos os pontos! De novo trouxe aqui um gráfico num ponto qualquer para não ficar dúvidas!
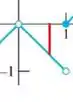
Então para todos os pontos desse intervalo o limite vai existir! Podemos dizer até mais: em todos os pontos desse intervalo (exceto o 0) o limite vale o mesmo valor da função no ponto e no , vale (lembra que , mas isso não faz diferença).
Passo 5
Vamos ver as afirmações que ele deu:
existe
Vimos que essa é verdadeira e que esse limite vale 0
Vimos que é verdade, mesmo com !
Isso é uma mentira deslavada! Só , mas perto do a função se aproxima de e não de !
Vimos que o limite em não existe, então não dá pra acreditar nisso... Falso!
Vimos que o limite em não existe, então essa é mais falsa que nota de
existe em todo em
Pode acreditar nessa aí!
não existe
Essa também está bonitona, verdadeiro!
Resposta
a) Verdadeiro
b) Verdadeiro
c) Falso
d) Falso
e) Falso
f) Verdadeiro
g) Verdadeiro