Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 29

Avalie a integral de superfície para o campo vetorial e a superfície . Em outras palavras, localize o fluxo de através de . Para superfícies fechadas, use a orientação (para o exterior) positiva.

é um cubo com vértices .

Passo 1

Faaaaala minha turminha, tudo na paz!?

Temos que calcualr o fluxo de através de .

Onde, é um cubo com vértices .

Nós temos aqui seis faces de um cubo, certo?

De acordo com a convenção, se a orientação não for dada, a gente assume que os vetores normais estão apontando na direção positiva. É bom notar que a área de cada face é unidades quadradas, isso acontece pois o cubo tem lado igual a . Veja a figura abaixo:

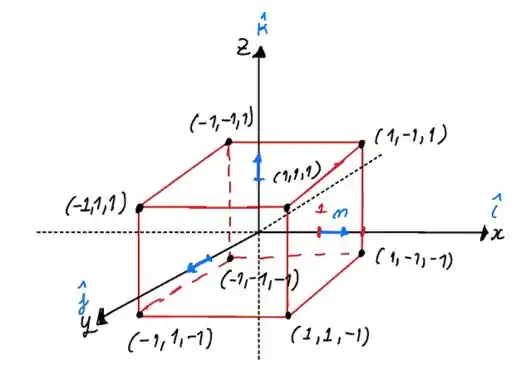
Para a face do cubo que está no plano :

onde é o vetor normal a face, que está apontando para fora do cubo. Assim,

Resolvendo o produto escalar, temos:

Notemos que em todos os pontos das superfícies.

Esse processo que fizemos, deve ser feito para cada face do cubo. Ai no final somamos todos os valores encontrados.

Repare que não é difícil, só vai ser trabalhaso. Então faça esse processo com calma.

Vamos nessa!

Passo 2

Agora, para a face do cubo que está no plano :

onde é o vetor normal a face, que está apontando para fora do cubo. Assim,

Notemos que em todos os pontos das superfícies.

Passo 3

Para a face do cubo que está no plano :

onde é o vetor normal a face, que está apontando para fora do cubo. Assim,

Notemos que em todos os pontos das superfícies.

Passo 4

Para a face do cubo que está no plano :

onde é o vetor normal a face, que está apontando para fora do cubo. Assim,

Notemos que em todos os pontos das superfícies.

Passo 5

Para a face do cubo que está no plano :

onde é o vetor normal a face, que está apontando para fora do cubo. Assim,

Notemos que em todos os pontos das superfícies.

Passo 6

Para a face do cubo que está no plano :

onde é o vetor normal a face, que está apontando para fora do cubo. Assim,

Notemos que em todos os pontos das superfícies.

Agora, para encontrar o fluxo somamos todos os valores encontrados. Desse jeito:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ S F.d S para o campo vetorial F e a superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação

Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu

Calcular I =∫ ∫ S x d y d z + y d z d x + z d x d y Onde S é a superfície exterior do cilindro x 2 + z 2 = a 2 Limitado pelos planos y =- 4 y = 4

Calcular ∫ ∫ S f → *n →d S Sendo f → = yi → - xj → e S a parte da esfera x 2 + y 2 + z 2 = a 2 no 1 octante com a normal apontando para fora

Calcular I =∫ ∫ S x 2 d y d z + y 2 d z d x + z 2 d x d y Onde S é a superfície exterior da semi-esfera x 2 + y 2 + z 2 = a 2 ,z ≥ 0