8 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Isso é,
ou
ou
ou
ou
Passo 2
Quando , o valor de , então o ponto crítico é .
Quando , o valor de , então o ponto crítico é .
Quando , então, o valor de , então, o ponto crítico é .
Portanto, os pontos críticos são:
Passo 3
b) O objetivo é desenhar um campo de direção e um retrato de fase para o sistema usando um computador.
Use o software de bordo para desenhar um campo de direção do sistema.
Primeiro escreva o sistema como,
O gráfico é mostrado abaixo:
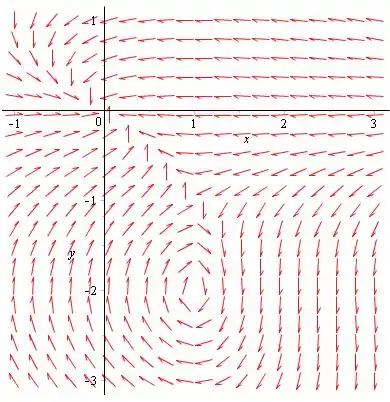
A figura acima é o campo de direção que contém e .
O ponto de espiral pode ser identificado abaixo:
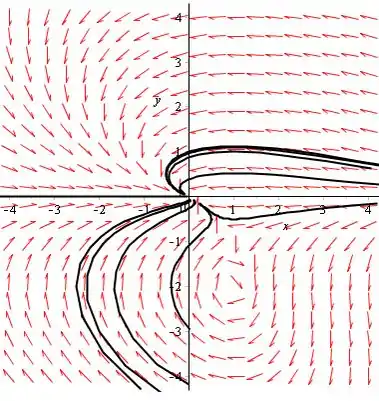
Passo 4
c) A partir da figura, o ponto é um ponto de espiral, é um afundamento nodal e é um ponto de sela. As trajetórias próximas ao ponto espiral se aproximam desse ponto , de modo que o ponto pode ser considerado assintoticamente estável. O campo de direção mostra que as trajetórias próximas ao nó estão se aproximando desse ponto, portanto, o ponto também é assintoticamente estável.
O ponto de sela é instável.
Passo 5
d)
O objetivo é descrever a bacia de atração para cada ponto crítico assintoticamente estável.
Lembre-se do conceito,
Seja qualquer ponto no plano com a propriedade pela qual uma trajetória passando se aproxima do ponto crítico. Como , então, diz-se que a trajetória é atraída pelo ponto crítico. O conjunto de todos esses pontos é chamado de bacia de atração ou região de estabilidade assintótica do ponto crítico.
Duas trajetórias entram no ponto de sela com inclinações de aproximadamente . Todas as outras trajetórias acabam saindo da vizinhança do ponto.
A linha é uma trajetória. Nesta linha, e é positivo ou negativo, dependendo de ser menor ou maior que .
Assim, nenhuma outra trajetória pode cruzar essa linha.
Resposta
- Os pontos críticos
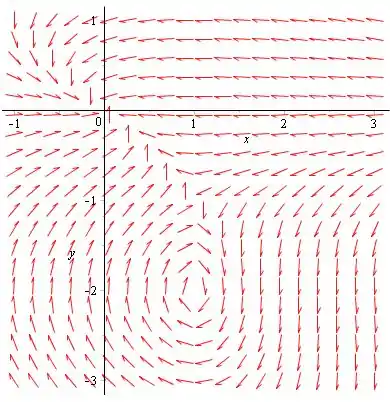
- O ponto crítico é um ponto espiral.
- Duas trajetórias entram no ponto de sela com inclinações de aproximadamente . Todas as outras trajetórias acabam saindo da vizinhança do ponto.
O ponto crítico é o ponto de nó e é assintoticamente estável.
O ponto crítico é um ponto de sela e instável.
A linha é uma trajetória. Nesta linha, e é positivo ou negativo, dependendo de ser menor ou maior que .
Assim, nenhuma outra trajetória pode cruzar essa linha.