Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 6
6 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Isso é,
e
Assim, existem dois pontos críticos e .
Passo 2
b) Use CAS, para esboçar o campo de direção e o retrato de fase do sistema.
Primeiro carregue o pacote, com (DEtools);
Entrada Maple:
Com a saída de bordo:
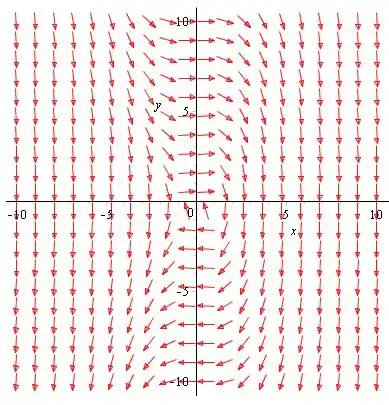
Passo 3
c) O objetivo é determinar o tipo e a estabilidade de cada um dos seguintes pontos críticos.
e .
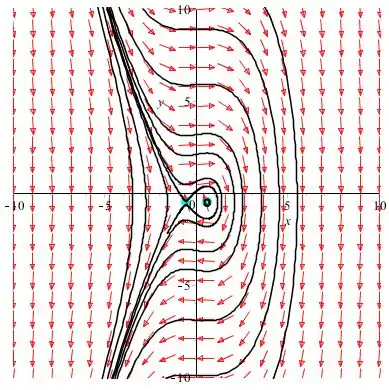
No diagrama acima, algumas curvas de solução são concêntricas com o ponto .
Portanto, este ponto é tratado como o centro do retrato de fase e é estável.
E, o ponto é um ponto de sela e é instável.
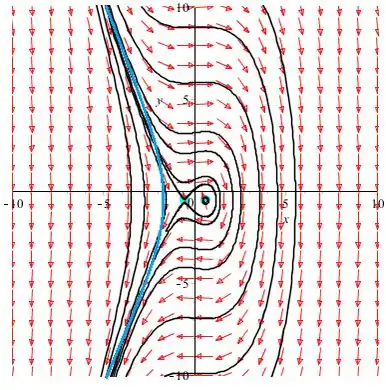
Observe que há uma separatriz mostrada na curva de cor azul que sai do ponto de sela como , circula em torno do centro e retorna ao ponto de sela como .
No lado direito da separatriz, as trajetórias estão ao redor do centro .
E no lado esquerdo da separatriz, as trajetórias são ilimitadas no ponto de equilíbrio.
Passo 4
d) A bacia de atração é o conjunto de todos os pontos em plano que possui a propriedade de que uma trajetória que começa e se aproxima do ponto crítico como .
O esboço da base de atração para o ponto assintoticamente estável é mostrado abaixo.
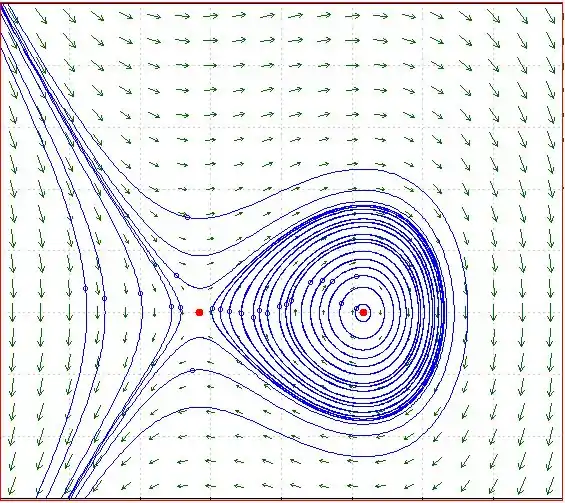
No esboço acima da bacia de atração, observe que as curvas da solução estão circundadas pelo ponto estável .
Resposta
a) existem dois pontos críticos e .
b)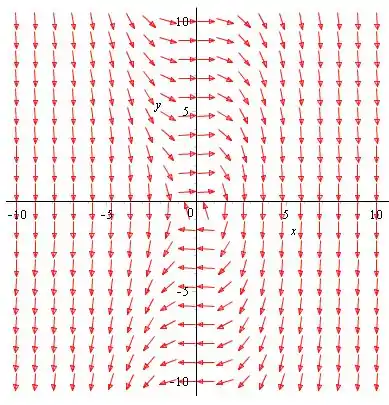 
c) O ponto é tratado como o centro do retrato de fase e é estável.
O ponto é um ponto de sela e é instável.
d)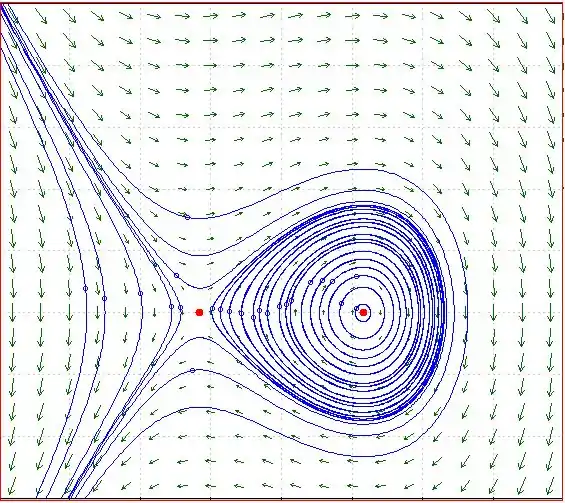 
No esboço acima da bacia de atração, observe que as curvas da solução estão circundadas pelo ponto estável .