Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 4
4. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas no intervalo .
a) não tem extremos relativos nem absolutos.
b) tem um mínimo absoluto em , mas nenhum máximo absoluto.
c) tem máximo e mínimo absolutos em e , respectivamente.
Passo 1
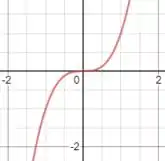
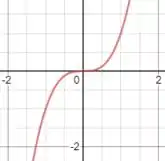
a) Então galera, aqui basta pegarmos uma função que não tenha picos. Para pensarmos em uma função desse tipo temos que colocar a cabeça pra funcionar mesmo, não tem jeito! Uma função interessante é:
Que possui um gráfico sem extremos relativos nem absolutos, saca só:
Passo 2
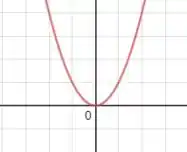
b) Aqui temos que pensar em uma função com concavidade para cima, no qual o mínimo se encontra em . Uma função boa seria , pois é uma função simétrica em relação ao eixo e tem mínimo em , se liga:
Passo 3
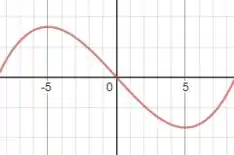
c) Aqui só temos que esboçar um gráfico que tenha dois picos: um pico é um máximo absoluto e está em e o outro pico é um mínimo absoluto que se encontra em . Uma função possível seria:
Que possui o esboço:
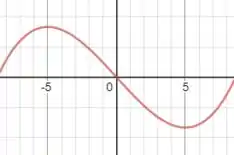
E estão aí nossos esboços, galera!
Resposta
c) 