Em cada um dos problemas de 9 a 12, encontre a solução do problema de valor inicial dado. Depois faça um gráfico da solução.

10.

Agora observem que como a equação ordinária dada no exercício, não está igualada a zero, temos um exemplo de EDO não homogênea. Então como temos quatro raízes complexas, teremos a seguinte homogênea associada:

Agora precisamos encontrar a nossa solução particular.

Dicazinha:É possível montar a solução particular, apenas trocando as constantes da homogênea associada, por outros parâmetros, aqui escolhi .

Repare que agora, precisamos de descobrir os valores de

Para isso, necessitamos do sistema de matrizes genérico:

Porém pela regra de Cramer, esse sistema pode ser convertido para seguinte expressão:

Aqui g(t) é a função da equação ordinária depois da igualdade (Aquela trazida lá no começo do problema!), correspondendo então, ao seguinte valor:

e é o determinante obtido desubstituindo a m-ésima coluna pela coluna

Calma que eu já te explico, vem comigo!

Vamos calcular primeiramente o determinante de W(t)

Lembram da nossa solução particular? De lá temos:

Que são as funções que acompanhamsacou?

Bora lá então e vamos inserir tudo isso na primeira linha, para derivarmos na sequência! . Isso porque temos 4 termos, n=4 e sempre diminuímos uma unidade desse valor, o que resulta em 3, assim precisaremos ir até a derivada de terceira ordem.

Agora precisamos descobrir o determinante de :

Repare que a única diferença para o cálculo de cada um desses determinantes, foi a posição da coluna (0,0,0,1).

Já que possuímos tudo que precisamos, vamos encontrar

Vamos resolver as integrais de do passo anterior, encontrando assim: .

Chegamos ao último passo! Agora podemos escrever a nossa solução particular, trocando , pelos respectivos valores encontrados no passo anterior. Assim teremos:

Portanto temos os dados necessários, para escrever a solução geral da equação diferencial que nos foi pedida. Esta será dada pela soma da homogênea associada com a solução particular encontrada. Dessa forma, teremos:

Note que somente o último termo da solução particular não é uma solução da equação homogênea.

Vamos resolver o problema de valor inicial pedido no exercício.

Vamos substituir a primeira condição de contorno na solução geral da equação diferencial.

A segunda condição de contorno, é dada por: . Dessa forma teremos:

A terceira condição de contorno, é dada por:

Sabemos que:

A quarta solução de contorno é que: , assim:

Temos as seguintes expressões e valores até aqui:

Da equação (2) temos que:

Substituindo (5) em (4) teremos:

Substituindo (6) em (5):

Vamos agora encontrar a solução geral do problema de valor inicial dado.

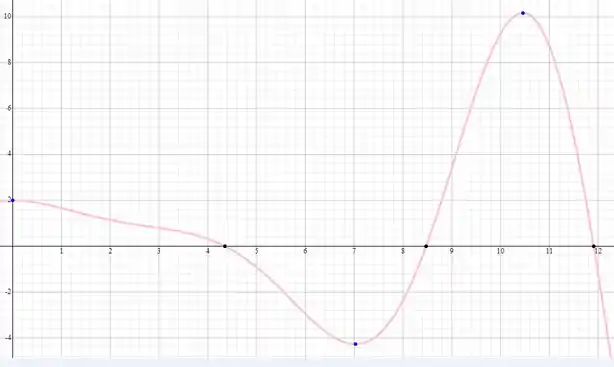
O gráfico da solução é portanto: