Cada um dos problemas 1 a 6 pode ser interpretado como descrevendo a interação de duas espécies com população x e y. E m cada um desses problemas, faça o seguinte:
a) Desenhe o campo de direções e descreva como as soluções parecem se comportar.
b) Encontro os pntos críticos.
c)Para cada ponto crítico, encontre o sistema linear correspondente. Encontre os autovalores e autovetores do sistema linear, classifique cada ponto crítico em relação ao tipo e determine se é assintoticamente estável, estável ou instável.
d) Esboce as trajetórias em uma vizinhança de cada ponto crítico.
e) Calcule e faça o gráfico de um número suficiente de trajetórias do sistema dado de modo a mostrarm claramente, o comportamento das soluções.
f) Determine o comportamento limite de x e y quando e interprete os resultados em termos das populações das suas espécies.
1.
Passo 1
a)
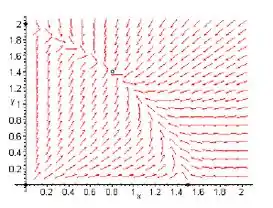
Passo 2
Os pontos críticos sçao soluções so distema de equações
Os 4 pontos críticos são então (0,0), (0,2), (1,5 , 0) e (0,8, 1,4) .
Passo 3
A matriz jacobiana do campo de vetories é
No ponto critico (0,0) o coeficiente matricial do sistema linearizado é dado por
Os autovalores e autovetores são
Os autovalores tem sinal oposto. Logo o ponto crítico é de sela, que é instável.
No ponto (1,5, 0) o coeficiente matriciano lineazrizado ficac
Os autovetores e autovalores são
Os autovalores tem sinal oposto. Logo o ponto crítico é de sela, que é instável.
No ponto (0,8 , 1,4) o coeficiente matriciano lineazrizado ficac
Os autovetores e autovalores são
Ambos os autovalores são negativos. Isso nos diz que o ponto crítico é um nó estável, que é assintoticamente estável.
Passo 4
d) e e)
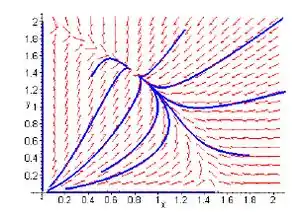
Passo 5
f) Exceto pelas condições iniciais que estão nos eixos coordenados, qualse toda trajetória converge para o ponto está vel em (0,8, 1,4).
Resposta
Ei, a resposta está no passo a passo :)