Exercícios de Retrato de Fase e Classificação de Ponto Crítico - Lista de Exercícios Resolvida
Questão 1
Sabendo que o ponto crítico do sistema abaixo é , determine o retrato de fase e qual tipo de ponto é o ponto crítico.
Ver solução completaQuestão 2
Seja . Considere as matrizes seguintes:
A seguir estão os retratos de fase dos sistemas
Ao lado de cada figura escreva qual é a letra da matriz correspondente.
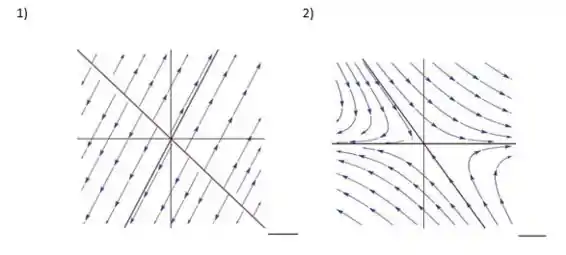
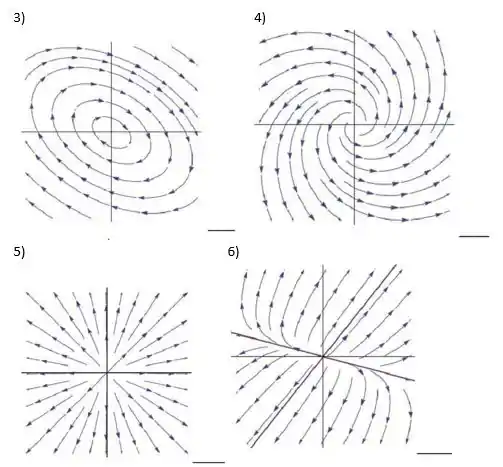
Questão 3
Considere o sistema linear onde:
Determine os valores de a, b para os quais:
I) As soluções do sistema satisfazem
II) A singularidade (0,0) é uma sela hiperbólica.
Ver solução completaQuestão 4
Considere o sistema .
a) Esboce o retrato de fase e classifique a singularidade (0,0).
b) Ache a solução geral do sistema onde:
c) Ache a solução do sistema da letra (b) com condição inicial
Ver solução completaQuestão 5
Seja . Considere as matrizes seguintes:
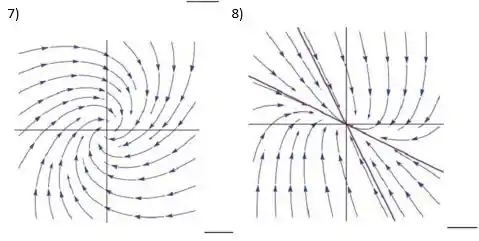
A seguir estão os retratos de fase dos sistemas
Ao lado de cada figura escreva qual é a letra da matriz correspondente.
1) 2)
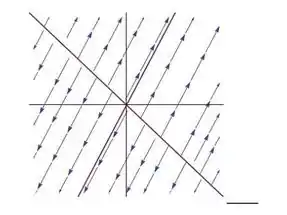
3) 4)
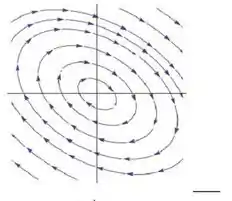
5) 6)
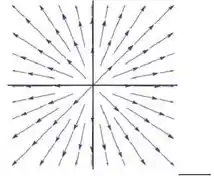
7) 8)
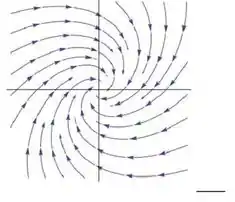
Questão 6
Considere o sistema linear onde:
Determine os valores do parâmetro real de maneira que no retrato de fase exista um nó atrativo.
Ver solução completaQuestão 7
Considere os autovalores e , e seus respectivos autovetores e de uma matriz .
Determine um sistema de equações diferenciais .
Esboce um retrato do sistema.
Esboce a trajetória que passa pelo ponto .
Ver solução completaQuestão 8
Considere a matriz dada por
Determine os valores de de modo que no retrato de fase do sistema o ponto crítico seja um centro.
Para , encontre a solução do sistema e esboce o retrato de fase.
Ver solução completa