Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 20a
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar:
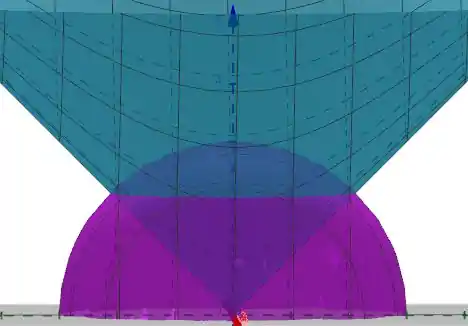
Beleza galera, já sabemos que a massa de um sólido pode ser calculada como:
O problema já nos disse que:
Então:
Agora nós só precisamos da integral, e para isso vamos delimitar o z, ok?
Pela figura nós vemos que o z vai do cone até a esfera:
Em coordenadas cilíndricas:
Então:
O raio será delimitado pelo encontro das figuras, concordam?
Então:
E o intervalo será:
O é o ângulo que o ponto pode fazer com o eixo x, na esfera esse ângulo vai de 0 até 360°:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo:
Na integral:
Sendo assim:
Para resolver esta integral vamos chamar:
Na integral:
De volta ao r:
Aplicando o intervalo:
Racionalizando:
Resolvendo a última integral:
No intervalo:
Substituindo o resultado da nossa integral na massa:
O que acharam desta?