Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 12

12 . Calcule a área da parte da superfície z   =   x y que se encontra dentro docilindro x 2   +   y 2   ≤   4   e fora do cilindro x 2   +   y 2   ≤   1

Passo 1

Pode até parecer confuso quando temos 2 equações, fica aquela dúvida de “qual superfície usar?”. Bem vamos traduzir o que esse exercício diz, temos então uma sela limitada por uma região.

E essa região limitada dessa sela que vamos calcular

. Lembrando que nossa estrutura de cálculo é

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Passo 2

Vamos calcular agora as derivadas parciais de z

z   =   x y  

z x = y

z y = x

Vamos Unir o que já calculamos a nossa integral

∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

∫ ∫ R ' 1 + x 2 + y 2 d y d x

SHOW!!!! Já temos nossa equação , vamos descobrir agora nossa região dada pelo enunciado

x 2   +   y 2   ≤   4

x 2   +   y 2 >   1

OU seja, é essa região abaixo

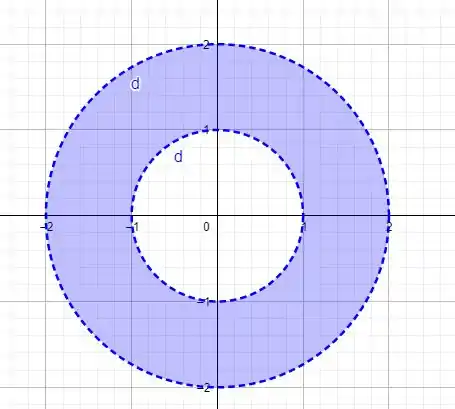
Uma rosquinha, hehe.

Passo 3

Como estamos em uma região circular. Seria mais fácil calcular em coordenadas polares, lembrando das transformações

x 2 + y 2 = r 2

J = r

Tendo então um intervalo de

1 < r < 2

0 < θ < 2 π

Vamos integral

∫ 0 2 π   ∫ 1 2 1 + r ²     r d r d θ

= 2 π *   1 3 1 + r 2 3 2 r = 1 2  

= 2 3 π   5 3 / 2 - 2 3 / 2

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x = 2 3 π   5 3 / 2 - 2 3 / 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2 . Seja A=0 ,y ,z ∈R 3z 2+y-2 2=1 } ; ache a área da superfíciegerada pela rotação em torno do eixo Oz do conjunto A.
7 . Calcule a área da superfície esférica x 2+y 2+z 2=2 que seencontra dentro do paraboloide z=x 2+y 2
4 . Calcule a área da parte da superfície cilíndrica z 2+x 2=4 que seencontra dentro do cilindro x 2+y 2≤4 e acima do plano xy
10 . Calcule a área de z = x 2 + y 2,x 2 + y 2 ≤ 2 x,x ≥ 1ey ≥ 0