Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 14
Calcule a integral dada, colocando-a em coordenadas polares.
14.
Onde é a região no primeiro quadrante que se encontra entre os círculos e .
Passo 1
Fala galera, beleza?
Precisamos calcular a integral como coordenada polar, como a questão pede, e também precisamos encontrar os limites de integração dessa região D através das informações no primeiro quadrante.
Show, né?
Pra começar, vamos lembrar as fórmulas que podemos utilizar nas coordenadas polares:
Olha só, pro primeiro círculo, com a equação:
Já sabemos que temos um círculo de raio centrado na origem:
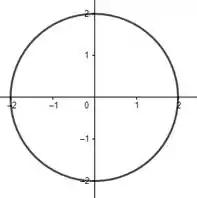
Agora pro segundo círculo:
Vamos precisar dar uma manipuladinha, saca só:
Vamos acrescentar , que não irá atrapalhar em nada:
Manipulando, teremos um produto notável:
Vamos ter, então, um círculo centrado em de raio :
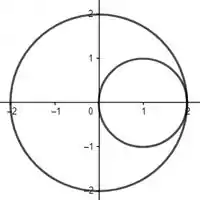
Como queremos a região no primeiro quadrante que esteja entre esses dois círculos, estamos falando desse vermelhão aqui:
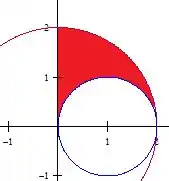
Show! Região entendida! Bora pras coordenadas polares!
Passo 2
Agora pra descrever a região em coordenadas polares, temos que achar como que varia e como que varia.
Pô, dando uma boa olhada na região , vemos que a menor distância radial que a região tem da origem é exatamente a circunferência menor:
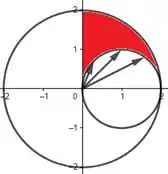
E a maior distância radial é justamente , que é o tamanho da circunferência maior:
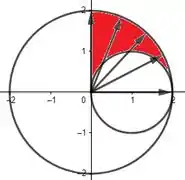
O intervalo de será então:
Como a circunferência menor tem essa equação:
E a mudança de coordenadas pras polares é:
Substituindo, achamos:
Fechou, o intervalo final será:
Agora, pro , é o seguinte:
Como definimos ele por ser o intervalo de abertura de determinado ângulo que contenha toda a região , sendo que essa abertura rola no sentido anti-horário partindo do Eixo no primeiro quadrante:
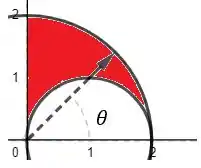
O intervalo que contém inteira é o próprio primeiro quadrante inteiro, logo:
Passo 3
Agora que sabemos os limites de integração, bora remontar a integral:
Substituindo tudo pelas expressões polares que estão lá em cima, temos que a integral fica:
Partiu integrar!
Passo 4
Vamos começar pela integral de dentro:
Agora, vamos analisar a integral de fora:
Colocando em evidência e depois jogando pra fora da integral a fração:
Daqui, poderemos dividir nossa integral em duas:
Vamos resolver logo a nossa primeira integral:
Agora, pra segunda integral, como:
Vamos ter:
A integral fica:
Podemos dividir nossa segunda integral assim:
Resolvendo essas integrais:
Descobrimos o valor da nossa segunda integral, agora unindo a primeira com a segunda teremos: