Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.4 - Ex. 12

Calcule a integral dada, colocando-a em coordenadas polares.

∬ R y e x   d A ,

onde R é a região do primeiro quadrante limitada pelo círculo x 2 + y 2 = 25 .

Passo 1

Fala minha turminha, tudo na paz? Vamos nessa!!

Devemos calcular a integral abaixo em coordenadas polares:

∬ R y e x   d A

Onde R é a região do primeiro quadrante limitada pelo círculo:

x 2 + y 2 = 25

Tá, mas e agora? Vamos pensar juntos!!!

Vamos lembrar onde fica o primeiro quadrante:

Sabemos que um círculo, certo? Ele disse isso. Vamos lembrar a expressão geral do círculo:

x 2 + y 2 = r 2

Só de comparar as duas expressões, já sabemos que o raio é 5 :

x 2 + y 2 = 5 2

Em coordenadas polares temos:

x = r cos ⁡ θ

y = r   s e n   θ

d A = d x d y = r d r d θ

Como queremos apenas no primeiro quadrante, o ângulo deve variar entre 0 e π 2 .

Logo nosso intervalo fica:

0 ≤ r ≤ 5

0 ≤ θ ≤ π / 2

Agora vai ficar fácil para você montar a integral em coordenadas polares ein! Depois é só resolver!

Bora lá!!!

Passo 2

Primeiro vamos passar a integral para coordenadas polares. Lembrando que:

x = r cos ⁡ θ

y = r   s e n   θ

d A = d x d y = r d r d θ

Substituindo na integral vamos ter:

∬ R y e x   d A

∬ R r 2   s e n   θ   e r cos ⁡ θ   d r   d θ

Agora devemos encontrar a região R , certo?

Já sabemos que é um círculo:

x 2 + y 2 = 5 2

x 2 + y 2 = r 2

Comparando com a equação geral concluímos que o raio é 5 . Como queremos somente a parcela do círculo que está no primeiro quadrante:

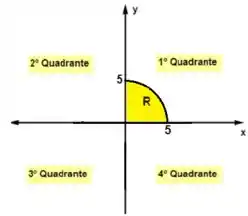
Concluímos que nosso intervalo de integração é:

0 ≤ r ≤ 5

0 ≤ θ ≤ π / 2

Substituindo na integral, ficamos com:

∫ 0 π 2 ∫ 0 5 r 2   s e n   θ   e r cos ⁡ θ   d r   d θ

Passo 3

Agora precisamos integrar, certo!? E você lembra que começamos de dentro para fora.

Mas para facilitar nossa vida, nesse caso, vamos mudar a ordem de integração. Ficando com:

∫ 0 5 ∫ 0 π 2 r 2   s e n   θ   e r cos ⁡ θ   d θ d r

Porque isso é possível? O teorema de Fubini explica isso:

Passo 4

Então, vamos começar integrando em d θ . E tudo que não depender de θ consideramos uma constante.

∫ 0 5 ∫ 0 π 2 r 2   s e n   θ   e r cos ⁡ θ   d θ d r

Vamos precisar, aplicar uma substituição do tipo:

u = r cos ⁡ θ

d u d θ = - r   s e n   θ   ∴   - d u = r   s e n   θ   d θ

Substituindo na integral temos que:

∫ 0 5 ∫ 0 π 2 r   e u   ( - d u ) d r

Integrando em d u e voltando para a variável θ , temos:

∫ 0 5 - r ( e r   c o s   θ ) 0 π 2 d r

Aplicando os limites de integração, ficamos com:

∫ 0 5 - r e r cos ⁡   π 2 - e r cos ⁡ 0 d r

Sabendo que:

cos ⁡ π 2 = 0 ;   cos ⁡ 0 = 1 ;   e 0 = 1

Simplificando, temos:

∫ 0 5 - r 1 - e r d r

Passo 5

Agora ficamos com uma integral simples em d r .

∫ 0 5 r e r - r d r

Aqui podemos separar em duas integrais, ficando:

∫ 0 5 r e r d r - ∫ 0 5 r d r

Para a primeira integral vamos ter que aplicar integração por partes, do tipo:

u v - ∫ v d u

Vamos escolher o u de tal forma que ao derivarmos ele vai reduzir seu grau. Podemos escolher assim:

u = r

d u = d r

d v = e r d r

∫ d v = ∫ e r d r

v = e r  

Substituindo, temos que:

r e r - ∫ 0 5 e r d r - ∫ 0 5 r d r

Integrando, temos:

r e r - e r - r 2 2 0 5

Aplicando os limites de integração e simplificando, ficamos com a seguinte resposta:

4 e 5 - 23 2

Resposta

4 e 5 - 23 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da região D de plano x y definida por D = x , y ∈ R 2 x 2 + y - 2 2 ≤ 4ex 2 + y 24 .
Calcule, usando mudança polar, as seguintes integrais: ∫ ∫ D x 2 + y 2 d x d y , onde D é a região no primeiro quadrante do pano x y limitada por x 2 + y 2 = 1 , x 2 + y 2 = 4 , y = x e y = 3 3 x .
Calcule, usando mudança polar, as seguintes integrais: ∫ ∫ D x 2 yd x d y , onde D = { ( x , y ) ∈ R 2 | x - 1 2 + y 2 ≤ 1 }
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .