Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.4 - Ex. 3

Calcule a integral indefinida.

int (d x)/(x sqrt(x^2 + 4))

Passo 1

Primeiramente vamos pegar o sqrt(x^2 + 4) e desenvolver a Identidade Pitagórica.

t = sqrt(x^2 + 4)

t^2 = x^2 + 4

t^2 = x^2 + 2^2

Montando o triângulo temos

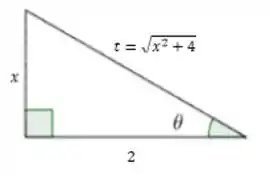
Com base nesse triângulo vamos usar a seguinte relação trigonométrica tan theta = (x)/(2)

Passo 2

Agora vamos aplicar a seguinte substituição chamar x = 2 tan theta e também as mudanças necessárias.

x = 2 tan theta

d x = 2 sec^2 theta d theta

int (2 sec^2 theta d theta)/(2 tan theta (sqrt((2 tan theta)^2 + 4)))

Passo 3

Vamos por alguns valores em evidência e aplicar a Identidade Trigonométrica.

int (2 sec^2 theta d theta)/(2 tan theta (sqrt(4 (tan^2 theta + 1))))

(cos^2 theta + sin^2 theta = 1) * (1)/(cos^2 theta)

1 + tan^2 theta = sec^2 theta

int (2 sec^2 theta d theta)/(2 tan theta * 2 sec theta)

(1)/(2) int (sec theta d theta)/(tan theta)

Passo 4

Aplicando a relação (1)/(tan theta) = cot theta = (cos theta)/(sin theta) trigonométrica temos

(1)/(2) int (cos theta sec theta d theta)/(sin theta)

(1)/(2) int (1 d theta)/(sin theta)

(1)/(2) int csc theta

Passo 5

Agora podemos resolver a integral e em seguida desfazer as mudanças através das relações trigonométricas do triângulo montado anteriormente cot theta = (2)/(x) e csc theta = (sqrt(x^2 + 4))/(x) .

(1)/(2) int csc theta

(1)/(2) ln (|csc theta - cot theta|) + c

(1)/(2) ln (|(sqrt(x^2 + 4))/(x) - (2)/(x)|) + c

(1)/(2) ln (|(sqrt(x^2 + 4) - 2)/(x)|) + c

(1)/(2) (ln (|sqrt(x^2 + 4) -|) - ln (|x|)) + c

Resposta

(1)/(2) (ln (|sqrt(x^2 + 4) -|) - ln (|x|)) + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral ∫ d x x 4 x 2 - 2 Coloque em um gráfico o integrando e a integral indefinida e verifique se sua resposta é razoável.
Calcule a integral ∫ x 1 - x 4d x
Calcule a integral ∫ 0 π 2 cos ⁡ t 1 + sin 2 ⁡ t d t
Uma barra carregada de comprimento L produz um campo elétrico no ponto P a , b dado por E P = ∫ - a L - a λ b 4 π ϵ 0 x 2 + b 2 3 2 d x Em que λ é a densidade de carga por unidade de comprimento da ba
Calcule a integral ∫ 1 3 1 + x 2 x 2 d x