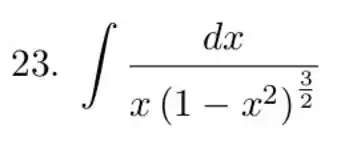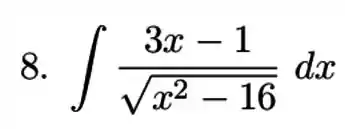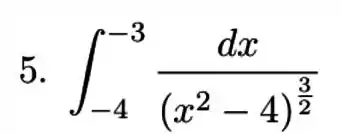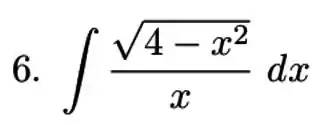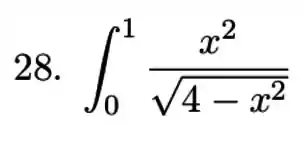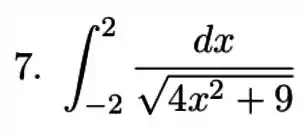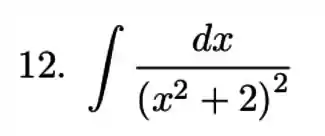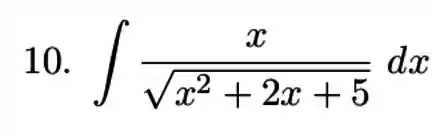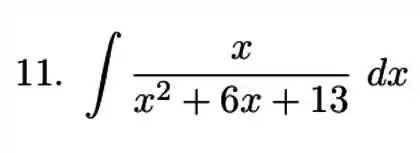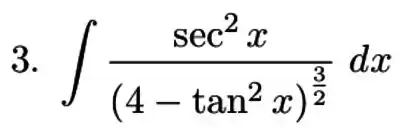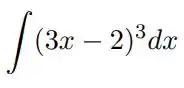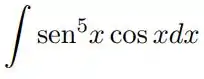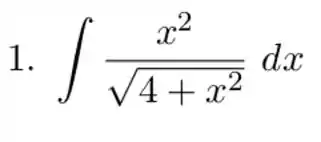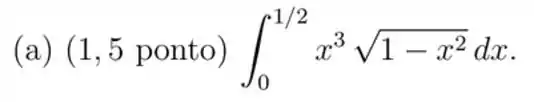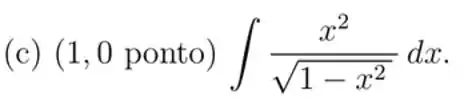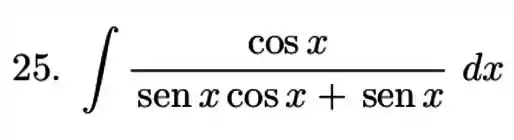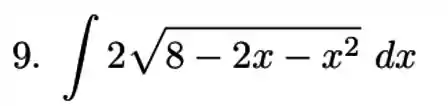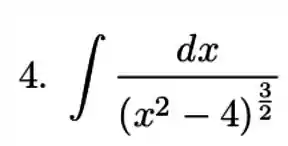Exercícios de Substituição Trigonométrica - Lista de Exercícios Resolvida
Questão 8
Calcular a integral
a) Na resolução desta integral utilizou-se a técnica de fração parcial, obtendo-se em uma das passagens de resolução os termos
b) Na resolução desta integral utilizou-se a técnica de integral por partes, obtendo-se em uma das passagens de resolução os termos
c) Na resolução desta integral utilizou-se a técnica de substituição de variáveis, obtendo-se em uma das passagens de resolução os termos
d) Na resolução desta integral utilizou-se a técnica de integração por substituição trigonométrica, obtendo-se em uma das passagens de resolução os termos
Ver solução completaQuestão 10
Calcular a integral
Na resolução desta integral utilizou-se a técnica de fração parcial, obtendo-se em uma das passagens de resolução os termos .
Na resolução desta integral utilizou-se a técnica de integral por partes, obtendo-se em uma das passagens de resolução os termos
Na resolução desta integral utilizou-se a técnica de substituição de variáveis, obtendo-se em uma das passagens de resolução os termos
Na resolução desta integral utilizou-se a técnica de integração por substituição trigonométrica, obtendo-se em uma das passagens de resolução os termos .
Ver solução completaQuestão 12
Seja uma função derivável, com derivada continua tal que para todo . Sabendo que e , o valor da integral:
É:
Ver solução completaQuestão 17
Calcular a integral
a) Na resolução desta integral utilizou-se a técnica de fração parcial, obtendo-se em uma das passagens de resolução os termos
b) Na resolução desta integral utilizou-se a técnica de integral por partes, obtendo-se em uma das passagens de resolução os termos
c) Na resolução desta integral utilizou-se a técnica de substituição de variáveis, obtendo-se em uma das passagens de resolução os termos
d) Na resolução desta integral utilizou-se a técnica de integração por substituição trigonométrica, obtendo-se em uma das passagens de resolução os termos
Ver solução completaQuestão 18
Calcular a integral
Na resolução desta integral utilizou-se a técnica de fração parcial, obtendo-se em uma das passagens de resolução os termos .
Na resolução desta integral utilizou-se a técnica de integral por partes, obtendo-se em uma das passagens de resolução os termos
Na resolução desta integral utilizou-se a técnica de substituição de variáveis, obtendo-se em uma das passagens de resolução os termos
Na resolução desta integral utilizou-se a técnica de integração por substituição trigonométrica, obtendo-se em uma das passagens de resolução os termos .
Ver solução completaQuestão 19
1) Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponda:
b)
Ver solução completaQuestão 20
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Ver solução completaQuestão 21
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Ver solução completaQuestão 25
1.7. Use uma substituição trigonométrica para calcular . Dica: represente como uma função envolvendo a partir da fórmula de prostaférese para calcular e da identidade trigonométrica fundamental.
Ver solução completaQuestão 37
4.3. Explique como você resolve uma integral do tipo no caso em que é par ou então é ímpar. Explique de duas formas: (i) usando a identidade trigonométrica que envolve e e (ii) fazendo a simplificação e . Se e , seu método funciona?
Ver solução completaQuestão 56
A eletricidade doméstica é fornecida na forma de corrente alternada que varia de a com uma frequência de 60 ciclos por segundo . A voltagem então, é dada pela seguinte equação
Onde é o tempo em segundos. Os voltímetros leem a voltagem RMS (raiz da média quadrática), que é a raiz quadrada do valor médio de em um ciclo.
Calcule a voltagem RMS da corrente doméstica
Muitos fornos elétricos requerem a voltagem RMS de . Encontre a amplitude correspondente necessária para a voltagem .
Ver solução completaQuestão 57
Resolva as integrais seguintes:
d) Inspirada na integral de Barack Obama (SQ1796)
Ver solução completaQuestão 61
Uma partícula se move em linha reta com função velocidade . Encontre sua função posição se
Ver solução completaQuestão 71
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
2)
Ver solução completaQuestão 85
- Calcule as integrais abaixo:
Dica: Utilize substituição trigonométrica.
Ver solução completaQuestão 96
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Ver solução completaQuestão 98
Calcule as integrais usando substituição trigonométrica. Esboce o triangulo retângulo.
b)
Ver solução completaQuestão 100
Calcule as integrais usando substituição trigonométrica. Esboce o triangulo retângulo.
Questão 109
Sejam um intervalo aberto contendo e uma função derivável, com derivada contínua, tal que e . Calcule
Ver solução completaQuestão 110
Seja uma função que admite derivadas de todas as ordens tal que para todo Sabendo-se que e que o valor de
Ver solução completaQuestão 114
Demonstre a fórmula para a área de um setor circular com raio e ângulo central .
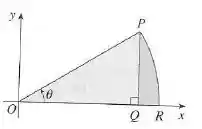
Questão 115
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado.
Ver solução completaQuestão 119
Um toro é gerado pela rotação do círculo ao redor do eixo . Ache o volume delimitado pelo toro.
Ver solução completaQuestão 132
1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(d)
Ver solução completaQuestão 133
1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(e)
Ver solução completaQuestão 134
1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(b)
Ver solução completaQuestão 137
1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(c)
Ver solução completaQuestão 147
Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponta:
a)
Ver solução completaQuestão 162
Calcule as integrais usando substituição trigonométrica. Esboce o triangulo retângulo.
c)
Ver solução completaQuestão 163
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Ver solução completaQuestão 165
Ache a área da região limitada pelos gráficos da parábola e a curva de Agnesi
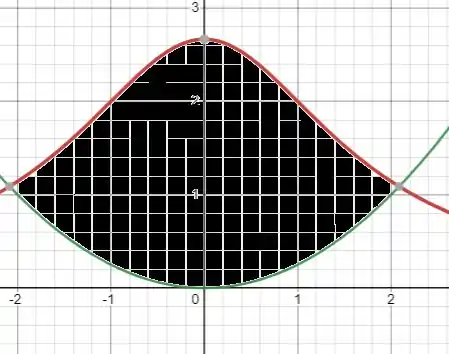
Questão 172
Seja uma função derivável, com derivada continua tal que para todo . Sabendo que e , o valor da integral:
É:
Ver solução completaQuestão 175
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Ver solução completaQuestão 176
1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(a)
Ver solução completaQuestão 181
2. Mediante o uso de uma tabela, calcule cada uma das seguintes integrais indefinidas.
Ver solução completaQuestão 187
A parábola divide o disco em duas partes. Encontre as áreas de ambas as partes.
Ver solução completaQuestão 189
Calcular as integrais usando o método da substituiç��o trigonométrica
Ver solução completaQuestão 190
Calcular as integrais usando o método da substituição trigonométrica
Ver solução completaQuestão 191
Calcular as integrais usando o método da substituição trigonométrica
Ver solução completaQuestão 192
Calcular as integrais usando o método da substituição trigonométrica
Ver solução completaQuestão 194
Calcular as integrais usando o método da substituição trigonométrica
Ver solução completaQuestão 198
5. Substituição Inversa
e)
Falaaa... beleza??
Nessa questão vamos calcular a integral
Como não é uma integral que conseguimos resolver diretamente, precisaremos de alguém método.
Um bizu maneiro é que quando tiver, dentro da integral, , ou (sendo um número e a variável), usamos substituição inversa, também conhecida como substituição trigonométrica.
Quando , usamos .
Quando , usamos
Quando , usamos ou .
Bora pra questão.
Ver solução completa