Calcule a integral de linha, onde é a curva dada.
consiste nos segmentos de reta de a e de a .
Passo 1
Fala, pessoal! Tudo certinho?
Então, nessa questão precisamos calcular essa integral de linha aqui, olha só:
Onde a região consiste nos segmentos de reta de a e de a que formam essa representação aqui:
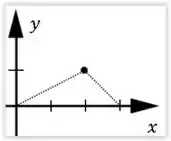
Pelo enunciado, o sentido do caminho é o horário. Outra coisa que devemos lembrar é como funciona uma integral de caminho. Devemos nos atentar que
Passo 2
Iniciamos nosso problema parametrizando as retas que iremos utilizar.
Para isso, vamos descobrir cada uma delas para cada ponto.
Quando vamos de para temos uma reta , assim como de para , .
Para a reta , vamos fazer um vetor do ponto
Assim,
Com isso, a equação da primeira reta parametrizada será dada por:
Escolhendo cada um dos pontos, chegaremos a
Assim temos:
Para a segunda reta, faremos a mesma coisa
Vamos chamar os pontos de
Chegamos a
Assim, nossa integral se transforma da seguinte maneira
Onde ambos os intervalos são descritos de a .
Passo 3
Vamos resolver primeiro e depois
Organizando,
Com isso ficamos com:
Show de bolinha 😉