Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 18

Calcular as integrais curvilíneas.

∫ C ( x - y )   d s , onde C é o triângulo da Figura 9.17 .

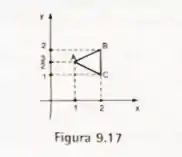
Passo 1

As coordenadas dos pontos são:

A = 1 , 3 2   ,   B = 2,2   e   C = ( 2,1 )

Vamos escrever as equações paramétricas das retas que passam por esses pontos.

Vamos chamar de:

  • C 1 : a   r e t a   q u e   p a s s a   p o r   A   e   B .
  • C 2 : a   r e t a   q u e   p a s s a   p o r   B   e   C .
  • C 3 : a   r e t a   q u e   p o r   A   e   C .

E aí nós fazemos a integral de linha de cada uma e no final somamos as três.

Passo 2

  • C 1 : A B → = 1 , 1 2

x = 1 + t y = 3 2 + 1 2 t   ,     t ∈ [ 0,1 ]

Vamos fazer a derivada disso agora:

C 1 ' = 1 , 1 2

E agora a norma...

C 1 ' = 1 2 + 1 2 2 = 5 2

Montamos a integral agora...

∫ 0 1 1 + t - 3 2 - 1 2 t 5 2 d t

∫ 0 1 1 2 t - 1 2 5 2 d t

5 4 t 2 2 - 5 4 t 0 1 = 5 8 - 5 4 =   - 5 8

Passo 3

Vamos para C 2 agora:

B C → = ( 0 , - 1 )

C 2 : x = 2 y = 2 - t ,   t ∈ [ 0,1 ]

Derivamos...

C 2 ' = 0 ,   - 1

E fazemos a norma para o d s ...

d s = 0 2 + - 1 2 = 1

Montamos a integral agora...

∫ 0 1 2 - 2 + t 1   d t

∫ 0 1 t   d t = t 2 2 0 1 = 1 2

Passo 4

Vamos para a C 3 agora...

C A → = - 1 , 1 2

C 3 : x = 2 - t y = 1 + 1 2 t     ,   t ∈ [ 0,1 ]

Vamos derivar agora...

C 3 = - 1 ,   1 2

Vamos fazer a norma agora para o d s :

d s = - 1 2 + 1 2 2 = 5 2

Vamos montar a integral agora...

∫ 0 1 2 - t - 1 - 1 2 t 5 2 d t

∫ 0 1 1 - 3 2 t 5 2 d t

5 2 t - 3 5 t 2 8 0 1

= 5 2 - 3 5 8 = 5 8

Somamos as três agora e...

- 5 8 + 1 2 + 5 8 = 1 2

Prontinho😊

Resposta

1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de linha, onde C é a curva dada. ∫ C xs e ny d s, Céos e g m e n t od er e t aq u el i g a0 ,3a( 4 ,6 ) é
Calcule a integral de linha, onde C é a curva dada. ∫ C x y 4 d s, Céam e t a d ed i r e i t ad oc í r c u l ox 2 + y 2 = 16 é í
Calcule a integral de linha, onde C é a curva dada. ∫ C x e y z d s, Céos e g m e n t od er e t ad e0 ,0 ,0a( 1 ,2 ,3 ) é
Calcule a integral de linha, onde C é a curva dada. ∫ C x y d s, C : x = t 2,y = 2 t,0 ≤ t ≤ 1
Calcule a integral de linha, onde C é a curva dada. ∫ C y 3 d s, C : x = t 3,y = t,0 ≤ t ≤ 2