Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 2

Calcule int_gamma vec F * d vec r , onde vec F (x , y) = (x + y^2) vec j e gamma é a curva do Exercício 1.

Passo 1

A curva do Exercício 1 é dada por

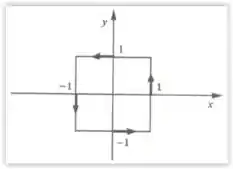
Tomando as parametrizações que utilizamos no exercício 1, temos

Vamos fazer assim

A curva superior gamma_1

gamma_1 (t) = (t , 1) , 1 >= t >= - 1

A curva a esquerda gamma_2

gamma_2 (t) = (- 1 , t) , 1 >= t >= - 1

A curva inferior gamma_3

gamma_3 (t) = (t , - 1) , - 1 <= t <= 1

A curva a direita gamma_4

gamma_4 (t) = (1 , t) , - 1 <= t <= 1

E é com esses valores que vamos resolver nosso problema.

Passo 2

Vamos fazer por partes.

Para gamma_1

vec F * d vec r = (0 , t + 1) * (d t , 0) = 0

Para gamma_2

vec F * d vec r = (0 , - 1 + t^2) * (0 , d t) = (t^2 - 1) d t

Para gamma_3

vec F * d vec r = (0 , t + (- 1)^2) * (d t , 0) = 0

Para gamma_4

vec F * d vec r = (0,1 + t^2) * (0 , d t) = (t^2 + 1) d t

Passo 3

Assim podemos reescrever a integral como

int_(- 1)^1 [- (t^2 - 1) + (t^2 + 1)] d t = int_(- 1)^1 2 d t = 2 (1 - (- 1)) = 4

O primeiro termo trocamos a ordem no intervalo pra escreve-lo em uma única integral. O sinal de negativo vem exatamente pois

int_a^b d x = - int_b^a d x

Resposta

4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o trabalho realizado pelo campo de força F → x , y = x 2 i ^ + y e x j ^ em uma partícula que se move sobre a parábola x = y 2 + 1 de ( 1,0 ) a ( 2,1 ) .
Calcule o valor da integral de linha, onde C é a curva dada.
Calcule o valor da integral de linha, onde C é a curva dada.
Calcule o valor da integral de linha, onde C é a curva dada.