Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 4
(a) Calcule a soma de Riemann para , e com seis termos, tomando os pontos amostrais como as extremidades direitas. (Dê a resposta correta até a sexta casa decimal). Explique o que a soma de Riemann representa com a ajuda de um esboço.
(b) Repita a parte (a) tomando como pontos amostrais os pontos médios.
Passo 1
Eaee, belezinha?? Bom... queremos calcular a soma de Riemann para a seguinte função:
No intervalo .
Onde devemos utilizar termos, tomando os pontos amostrais como as extremidades direitas.
Para isso, devemos saber que a soma de Riemann é um método matemático usado para aproximar a integral de uma função definida em um intervalo específico.
A soma de Riemann para aproximar uma integral de uma função definida no intervalo é dada da seguinte forma:
Em que e .
Onde é o número de subintervalos (ou termos) e é a largura do subintervalo.
Em seguida, devemos explicar o que a soma de Riemann representa com a ajuda de um esboço.
Por fim, devemos repetir o que fizemos, mas utilizando os pontos médios como pontos amostrais
Agora vamos aplicar!! 😉
Passo 2
Com teremos que:
e é um ponto extremo esquerdo.
Como nossa função varia de a , então:
Passo 3
Assim, aplicando a soma de Riemann para termos, temos:
Passo 4
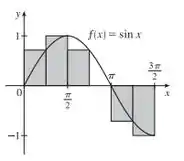
A soma de Riemann representa a soma das áreas dos três retângulos sobre o eixo menos a soma das áreas dos dois retângulos abaixo do eixo , isto é a “área líquida” dos retângulos com respeito ao eixo .
O diagrama formado é o seguinte:
Passo 5
Agora usando os pontos médios, temos que:
Assim, aplicando a soma de Riemann, temos:
Passo 6
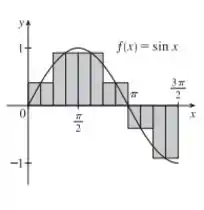
A soma de Riemann representa a soma das áreas dos quatro retângulos sobre o eixo menos a soma das áreas dos dois retângulos abaixo do eixo , isto é a “área líquida” dos retângulos com respeito ao eixo .
O diagrama formado é o seguinte:
Resposta
- Soma:
- Soma:
A soma de Riemann representa a soma das áreas dos três retângulos sobre o eixo menos a soma das áreas dos dois retângulos abaixo do eixo , isto é a “área líquida” dos retângulos com respeito ao eixo .
A soma de Riemann representa a soma das áreas dos quatro retângulos sobre o eixo menos a soma das áreas dos dois retângulos abaixo do eixo , isto é a “área líquida” dos retângulos com respeito ao eixo .