Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.4 - Ex. 1i

Calcule

i) int int int_B x * d x * d y * d z onde B é o conjunto x^2 + y^2 <= 4 , x >= 0 e x + y <= z <= x + y + 1 .

Passo 1

Nesse problema iremos reduzir o problema de uma integral tripla para uma dupla analisando os limites de integração para cada variável. Após reduzirmos para uma forma simplificada, vamos encontrar qual é o novo conjunto K , aplicando, caso necessário, uma transformação de variável.

Passo 2

Bom, vamos começar. Vemos que a integral dada pode ser reduzida. Conseguimos notar que z varia em um intervalo dado já. Assim, podemos escrever a integral tripla como

int int int_B x * d x * d y * d z = int int_K x * [int_(x + y)^(x + y + 1) d z] * d x * d y

Por sorte, podemos notar já que o resultado da integral em z será 1 (sempre é bom quando o resultado dá 1 ou 0 , né? Hehe...). Observando o domínio em K teremos que o conjunto será dado por x^2 + y^2 <= 4 , x >= 0 . Precisamos notar aqui que o fato de o enunciado dizer que x >= 0 é muito importante, pois isso quer dizer que não teremos valores negativos para x , assim a nossa circunferência será algo desse tipo.

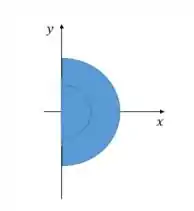
Assim, se aplicarmos uma transformação para coordenadas polares, nossos intervalos de integração ficarão

x = rho * cos theta

y = rho * sin theta

(3 * pi)/(4) <= theta <= (pi)/(2)

0 <= rho <= 2

O jacobiano dá transformação será o dado pelas coordenadas polares, onde d x * d y = rho * d rho * d theta . Finalmente podemos resolver a integral, que será

int int_K x * d x * d y = int_((3 * pi)/(4))^((pi)/(2)) int_0^2 (rho * cos theta) * rho * d rho * d theta = int_((3 * pi)/(4))^((pi)/(2)) cos theta * d theta * int rho^2 * d rho =

= [sin theta]_((3 * pi)/(4))^((pi)/(2)) * (8)/(3) = (16)/(3)

Resposta

int int int_B x * d x * d y * d z = (16)/(3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os volumes das regiões nos Exercícios 23-36.O tetraedro no primeiro octante delimitado pelos planos coordenados e o plano passando por (1, 0, 0), (0, 2, 0) e (0, 0, 3)
Encontre os volumes das regiões nos Exercícios 23-36.A região finita delimitada pelos planos z = x, x + z = 8, z = y,y = 8 e z = 0
Encontre os volumes das regiões nos Exercícios 23-36.A região no primeiro octante delimitada pelos planos coordenados, o plano y = 1 – x e a superfície z = cos (px/2), 0 ≤ x ≤ 1
Encontre os volumes das regiões nos Exercícios 23-36.A cunha cortada do cilindro x2 + y2 = 1 pelos planos z = –ye z = 0
Calcule as integrais nos Exercícios 41-44 alterando a ordem de integração de maneira apropriada. ∫ 0 4   ∫ 0 1   ∫ 2 y 2   4 c o s ⁡ x 2 2 z d x d y d z