Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.Revisão - Ex. 18
Considere o sólido obtido quando a região englobada por e gira em torno do eixo . Sem efetuar uma integração, encontre o valor médio da área de uma seção
transversal desse sólido tomada perpendicularmente ao eixo .
Passo 1
A figura que representa esse problema, é:
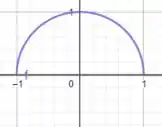
Vamos começar calculando a área:
Passo 2
Assim, finalizamos aplicando uma integração:
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Demonstre o Teorema do Valor Médio para Integrais usando o Teorema do Valor Médio para derivadas (veja a Seção 4.2) para a função F x = ∫ a x f ( t ) d t .
A velocidade v do sangue que circula em uma veia com raio R e comprimento l a uma distância r do eixo central é v r = P 4 η l R 2 - r 2 em que P é a diferença de pressão entre as extremidades da veia
Uma xícara de café tem temperatura de 95º C º e leva 30 minutos para esfriar até 61º C º em uma sala com temperatura de 20º C º . Use a Lei de Newton do Resfriamento (Seção 3.8) para mostrar que a tem
Se um corpo em queda livre parte do repouso, então o seu deslocamento é dado por s = 1 2 g t ² ². Seja v t a velocidade após um tempo T . Mostre que, se calcularmos a média das velocidades em relação
Se f med [ a , b ] denota o valor médio de f no intervalo [ a , b ] e acb , mostre que f med a , b = c - a b - a f med a , c + b - c b - a f med [ c , b ]