Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 1

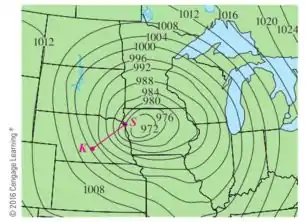
As curvas de nível da pressão barométrica (em milibares) são mostradas às da manhã de um dia de novembro. Uma baixa profunda com pressão de está se movendo sobre o nordeste de Iowa. A distância ao longo da linha vermelha de (Kearney, Nebraska) para (Sioux City, Iowa) é de . Estime o valor da derivada direcional da função de pressão em Kearney na direção de Sioux City. Quais são as unidades da derivada direcional?

Passo 1

Faaaala galera! Nessa questão nós temos um gráfico que mostra as curvas de nível para diferentes valores de pressão.

A partir desse gráfico nós queremos determinar a taxa de variação de pressão na direção que liga os pontos e mostrados no gráfico acima.

Como não temos uma expressão da pressão em função da posição, teremos que fazer isso por estimativa. Uma boa estimativa será tirar a taxa média de mudança de pressão entre os pontos onde a linha rosa cruza inicialmente.

Passo 2

A pressão inicial em é e, em seguida, a próxima curva de nível de pressão é .

Como se trata de uma reta, sabemos que a pressão varia na mesma proporção. Mas como sabemos a distância da curva em até a curva em ?

A questão diz que de até há aproximadamente , então se considerarmos que a distância entre uma curva e outra seja aproximadamente constante, teremos que a nossa distância entre as curvas de e será de aproximadamente .

Sendo assim, nossa derivada direcional será:

E a unidade da derivada direcional será:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 2 a 6 , calcular, usando a definição, a derivada direcional no ponto e direção indicados:5. f x , y = 2 - x 2 - y 2 , P ( 1 ,1 ) , na direção do vetor tangente unitário à curva C : r →

Nos exercícios 2 a 6, calcular, usando a definição, a derivada direcional no ponto e direção indicados.6. f x ,y ,z = 2 x + 3 y - z ,P 1 ,1 ,- 1 na direção do eixo positivo dos y .

12. O Capitão Astro está outra vez em perigo perto da orbita de Mercúrio. Ele está na posição P 0 = ( 1,1 , 1 ) , e a temperatura de blindagem de sua espaçonave num ponto ( x , y , z ) é dada por T x

6- Seja f x ,y = x y x 2 + y 2 ,x ,y ≠ ( 0,0 ) 0 ,x ,y = ( 0,0 ) Mostre que:c) f ( x ,y ) possui derivadas direcionais em todas as direções no ponto 0 ,0 .