Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 15
Defina as integrais iteradas para ambas as ordens de integração. Então, calcule a integral dupla usando a ordem mais fácil e explique porque ela é mais fácil.
Passo 1
E aí, amigos! Tudo certinho?
A questão pede para achar as integrais iteradas, para as duas ordens de integração. Depois, vamos precisar entender qual das duas ordens torna nosso cálculo de integral mais fácil e porquê. A integral que vamos precisar calcular é:
Para encontrar os limites de integração para cada variável ( e ) vamos ter que plotar a região e entendermos quais os limites de integração vamos precisar pegar, então vamos começar plotando:
Podemos integrar uma região como uma região do tipo I ou II:
- Regiões do Tipo I: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
- Regiões do Tipo II: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar abaixo da outra no eixo , assim a região fica confinada entre e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar antes da outra no eixo , assim a região fica confinada entre e .
Vamo que vamo!
Passo 2
Oi pessoal, tudo bem? Vamos analisar essa questão.
Como é limitado pelas retas e , vamos plotar estas retas para ver como fica a região :
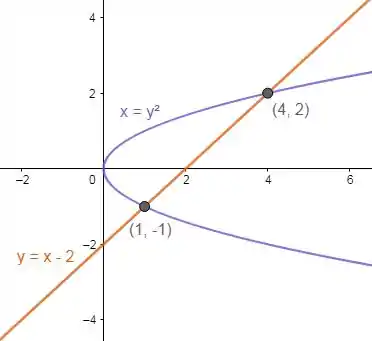
Nosso objetivo é expressar como uma região do tipo e também do tipo e em seguida analisar qual a integral dupla que será mais fácil de resolver.
Passo 3
Para a região como do tipo , temos:
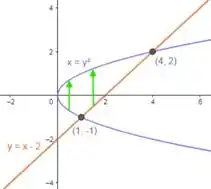
Aqui vamos precisar definir nossa região do tipo I pela união de dois intervalos diferente, já que entre os valores de de e , nossa função inferior é , entre de 1 a 4, nossa função inferior é .
Note que tínhamos a curva:
Deixando em função de , aplicamos a raiz quadrada dos dois lados para isolarmos e ficamos com:
Então:
Temos então que:
Passo 4
Para a região como do tipo , temos:
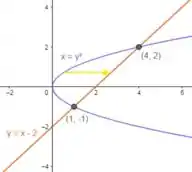
Colocando em função de , isolamos:
Temos então que:
Passo 5
Podemos notar que a integral gerada a partir da região do tipo é mais complicada porque o limite inferior consiste em duas partes diferentes. Então vamos resolver para o tipo .
Temos então que:
Vamos resolver a integral de dentro:
Logo:
Resolvendo, temos:
Portanto: