Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.4 - Ex. 10
Desenhe o gráfico de e de seu plano tangente no ponto dado. (Utilize um sistema de computação algébrica tanto para calcular as derivadas parciais quanto para traçar os gráficos da função e de seu plano tangente.) Em seguida, dê zoom até que a superfície e o plano tangente perto do ponto se tornem indistinguíveis.
Passo 1
Eaeee, tudo tranquilinho??? Bom... o enunciado nos deu essa função (bem cabulosa haha):
Queremos elaborar o gráfico de e também o gráfico do plano tangente ao ponto .
Lembrando que, para isso, temos a seguinte fórmula geral para uma equação do plano tangente a uma superfície no ponto :
Dessa forma, podemos inferir que:
Assim, só nos resta calcular as derivadas parciais e , bem como plotar os gráficos!!!
Simples né??....Brincadeeeira haha.
Aqui a gente vai utilizar alguma ferramenta computacional tanto para gerar os gráficos quanto para calcular as derivadas (o enunciado nos pede isso).
Agora bora lá!! 😉
Passo 2
Bom... ao aplicar em um software matemático, encontramos a seguinte derivada :
Aplicando o ponto dado, temos:
Agora vamos fazer o mesmo para .
Passo 3
Bom... ao aplicar em um software matemático, encontramos a seguinte derivada :
Aplicando o ponto dado, temos:
Passo 4
Do Passo 1, vimos a seguinte expressão para o plano tangente em um ponto genérico:
Desta forma, substituindo os valores que encontramos, temos:
Passo 5
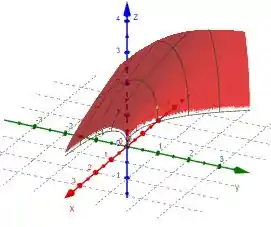
Plotando o gráfico da nossa função , temos:
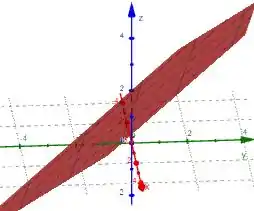
Traçando agora o gráfico do plano tangente, temos:
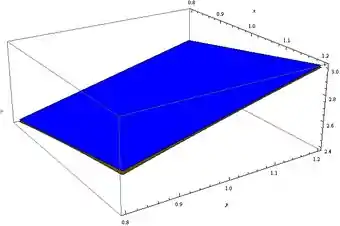
Se a gente colocar os dois juntos e der um zoom no ponto dado até eles ficarem quase indistinguíveis, teremos:
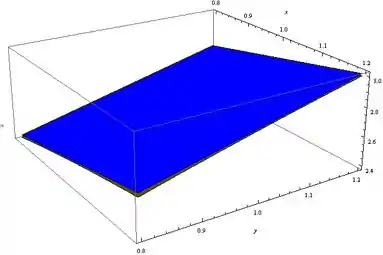
Obs: o gráfico do plano agora é dado em azul.
Resposta
Gráfico de :
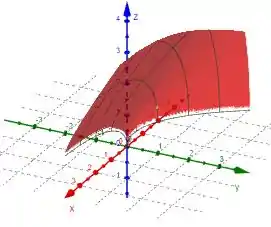
Gráfico do plano:
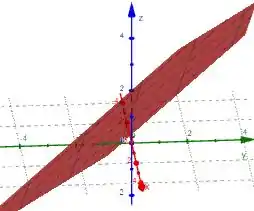
Zoom aplicado no ponto dado:
