Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 7
Determine a imagem do conjunto sob a transformação dada.
Passo 1
Faala, pessoal!
Essa questão pede pra acharmos a imagem de uma transformação...
Bom, essa transformação que ela da pega pontos de e leva em valores de .
O que a gente precisa achar é, se aplicarmos essa transformação pra todos os pontos de , nós vamos chegar a uma região , dos pontos .
Mas calma, que a gente não precisa calcular em todos os pontos (nem iríamos conseguir haha). Basta calcularmos nos limites da região!
Ou seja, vamos começar desenhando a região , e vendo como que os limites dessa região ficam após a transformação!
Passo 2
Bom, nossa região é um retângulo:
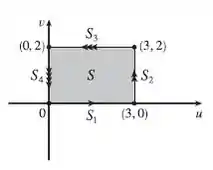
Vamos olhar pra cada uma dessas retas , e ver no que que elas se transformam.
Então primeiro vamos olhar para o lado no plano . é descrito por , e das equações dadas temos:
Substituindo na primeira ficamos com:
E como ,
Passo 3
é o segmento de reta , então:
Então isolando na segunda equação, e substituindo na primeira:
Como :
Passo 4
é o segmento de reta , então:
Isolando na segunda equação e substituindo na primeira vamos ficar com:
Como :
Passo 5
E por último, é o segmento , então ficamos com:
E substituindo em :
Como :
Passo 6
Então nossas retas são:
Vamos desenhar essas retas nos intervalos de correspondentes:
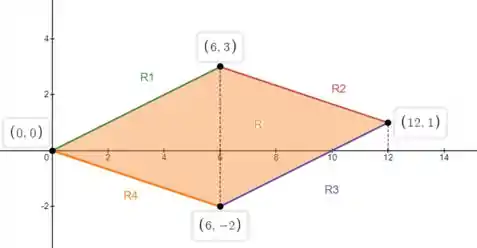
Então, a imagem de é o paralelogramo de vértices .
Resposta
O paralelogramo de vértices