Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 36

Determine a massa e o centro de massa de um arame com formato da hélice x = t   ,     y = cos ⁡ t   ,     z = s e n   t   ,     0 ≤ t ≤ 2 π   , se a densidade em qualquer ponto for igual ao quadrado da sua distância do ponto à origem.

Passo 1

Faaaala minha turminha, belezinha!? Vamos lá!

Nesse exercício temos que calcular a massa e o centro de massa de um arame em forma de hélice. As expressões parametrizadas dessa hélice são:

x = t   ,     y = cos ⁡ t   ,     z = s e n   t   ,     0 ≤ t ≤ 2 π

A densidade em qualquer ponto é igual ao quadrado da sua distância do ponto à origem.

Vamos plotar com o Geogebra para entender como fica essa figura. Vamos ter:

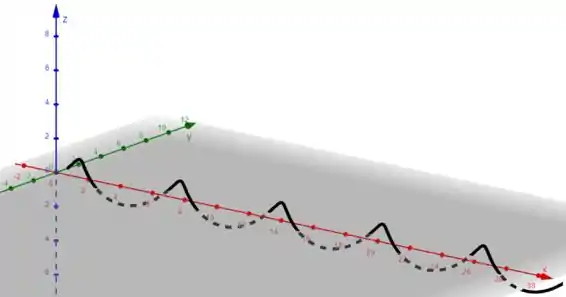
Podemos relacionar como se fosse um cilindro no eixo x , e essa hélice estivesse percorrendo na borda desse cilindro. Desse jeito:

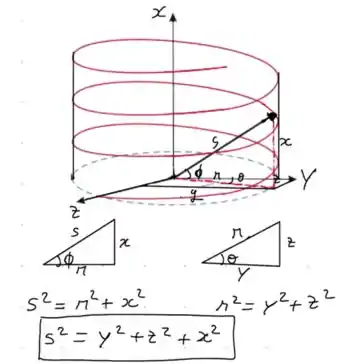
Só fazendo relação de triângulos, conseguimos achar a distancia da origem até um ponto da hélice. Assim, chegamos à conclusão que a densidade é:

ρ x ,   y ,   z = x 2 + y 2 + z 2 = t 2 + cos 2 ⁡ t + s e n 2   t = t 2 + 1

Sabemos que a massa m e os centro de massas x - ,   y - , são obtidos através das seguintes fórmulas:

m = ∬ D   ρ ( x ,   y , z )   d A

x - = ∬ D   x   ρ x ,   y , z   d A m

y - = ∬ D   y   ρ x ,   y , z   d A m

z - = ∬ D   z   ρ x ,   y , z   d A m

Porem como estamos trabalhando com uma curva parametrizada, vamos transcrever essa integral dupla em integral de linha. Ficando:

x - = ∫ C x   ρ ( x ,   y ,   z ) d s m

y - = ∫ C y   ρ ( x ,   y ,   z ) d s m

z - = ∫ C z   ρ ( x ,   y ,   z ) d s m

Agora é só você começar a calcular! Comece determinando a massa e depois encontre o centro de massa!

Vamos começar!

Passo 2

Começando determinando a massa:

m = ∫ C ρ ( x ,   y ,   z )   d s

Como vimos antes a densidade pode ser escrita como:

ρ x ,   y ,   z = t 2 + 1

Esse tipo de integral na forma parametrizada tem essa cara:

m = ∫ C ρ ( x ,   y ,   z )   d s = ∫ C ρ ( x ( t ) ,   y ( t ) ,   z ( t ) ) d x d t 2 + d y d t 2 + d z d t 2   d t

Repare, que já temos nossa função densidade parametrizada. Agora precisamos aplicar as derivadas da parametrização ao quadrado na raiz.

A parametrização da hélice foi dada no enunciado. Ela é:

r t = x ,   cos ⁡ t ,   s e n   t ,     0 ≤ t ≤ 2 π  

Fazendo as derivadas e aplicando em d s , vamos ter:

1 2 + - s e n   t 2 + cos ⁡ t 2   d t = 2   d t

Então a integral vai ficar assim:

m = ∫ 0 2 π   t 2 + 1 2 d t

Integrando em relação a d t , vamos ter:

m =   2 t 3 3 + t 0 2 π

Aplicando os limites de integração, temos que a massa vale:

m = 2 8 π 3 3 + 2 π

Passo 3

Agora vamos calcular cada uma das coordenadas do centro de massa, começando com x - .

x - = ∫ C x   ρ ( x ,   y ,   z ) d s m

Substituindo na integral os valores dos termos que obtemos nos passos anteriores, vamos ficar com:

x - = ∫ 0 2 π 2   t 2 + 1 t   d t 2 8 π 3 3 + 2 π

Simplificando um pouco temos:

x - = 1 8 π 3 3 + 2 π ∫ 0 2 π   t 3 + t d t

Integrando em d t , vamos ter:

x - = 1 8 π 3 3 + 2 π t 4 4 + t 2 2 0 2 π

Aplicando os limites de integração, ficamos com:

x - = 4 π 4 + 2 π 2 8 π 3 3 + 2 π

Vamos tentar simplificar mais, tirando o mínimo múltiplo comum no denominador e dividindo tudo por π . Logo vamos ter:

x - = 4 π 3 + 2 π 1 3 8 π 2 + 6

Dividindo tudo por 2 e reorganizando, vamos ter:

x - = 6 π 3 + 3 π 4 π 2 + 3

Passo 4

Agora vamos determinar o y - :

y - = ∫ C y   ρ ( x ,   y ,   z ) d s m

Substituindo na integral os termos, vamos ter:

y - = ∫ 0 2 π cos ⁡ t   t 2 + 1 2   d t 2 8 π 3 3 + 2 π

Reorganizando, vamos ter:

y - = 1 8 π 3 3 + 2 π ∫ 0 2 π   t 2 cos ⁡ t + cos ⁡ t d t

Agora vamos ter que separar em duas integrais para facilitar. Ficando assim:

y - = 1 8 π 3 3 + 2 π ∫ 0 2 π   t 2 cos ⁡ t d t + ∫ 0 2 π   cos ⁡ t d t

Na primeira integral devemos aplicar integrais por partes duas vezes, então vamos com calma para não errar nada.

Passo 5

Vamos resolver somente essa integral, depois voltamos para a expressão toda, certo?

∫ t 2 cos ⁡ t   d t

Vamos chamar:

u = t 2

d u = 2 t d t

d v = cos ⁡ t   d t

v = s e n   t

Devemos substituir em:

u v - ∫ v d u

Substituindo, temos:

t 2 s e n   t - ∫ 2 t   s e n   t   d t

Fazendo novamente integrais por partes, temos que:

u = 2 t

d u = 2 d t

d v = s e n   t   d t

v = - cos ⁡ t

Aplicando em:

u v - ∫ v d u

Temos que:

t 2 s e n   t - - 2 t c o s   t - ∫ - 2 cos ⁡ t   d t

t 2 s e n   t + 2 t c o s   t - 2 ∫ cos ⁡ t   d t

Integrando novamente, vamos ter:

t 2 s e n   t + 2 t c o s   t - 2 s e n   t

Encontramos que a integral de:

∫ t 2 cos ⁡ t   d t = t 2 s e n   t + 2 t c o s �� t - 2 s e n   t

Passo 6

Voltando para nossa integral do centro de massa em y .

Substituindo a integral que encontramos antes temos:

y - = 1 8 π 3 3 + 2 π t 2 s e n   t + 2 t c o s   t - 2 s e n   t + ∫ 0 2 π   cos ⁡ t d t

Integrando a integral que restou, temos que:

y - = 1 8 π 3 3 + 2 π t 2 s e n   t + 2 t c o s   t - s e n   t 0 2 π

Aplicando os limites de integração temos:

y - = 1 8 π 3 3 + 2 π ( 2 π ) 2 s e n   2 π + 2 ( 2 π ) c o s   2 π - s e n   2 π - ( 0 + 0 - s e n   0

Resolvendo, vamos ter que:

y - = 1 8 π 3 3 + 2 π 4 π

Simplificando, vamos ter:

y - = 6 4 π 2 + 3

Passo 7

Por último, vamos calcular o centro de massa em z - :

z - = ∫ C z   ρ ( x ,   y ,   z ) d s m

Substituindo as variáveis, vamos ter:

z - = ∫ 0 2 π 2   t 2 + 1   s e n   t   d t 2 8 π 3 3 + 2 π

Simplificando, vamos ter:

z - = 1 8 π 3 3 + 2 π ∫ 0 2 π t 2   s e n   t + s e n   t   d t

Vamos separar novamente em duas integrais para facilitar.

z - = 1 8 π 3 3 + 2 π ∫ 0 2 π t 2   s e n   t   d t +   ∫ 0 2 π s e n   t   d t

Repare que novamente vamos ter que aplicar duas vezes integrais por partes. O processo vai ser exatamente igual ao que fizemos antes para no calculo do y - .

Vamos polpar tempo e espaço nesse caso, você viu passo a passo o procedimento acima.

Aplicando duas vezes integrais por partes, vamos chegar na seguinte resposta:

∫ 0 2 π t 2   s e n   t   d t = - t 2 cos ⁡ t + 2 cos ⁡ t + 2 t   s e n   t

Substituindo na integral, vamos ter:

z - = 1 8 π 3 3 + 2 π - t 2 cos ⁡ t + 2 cos ⁡ t + 2 t   s e n   t +   ∫ 0 2 π s e n   t   d t

Resolvendo a última integral, temos:

z - = 1 8 π 3 3 + 2 π - t 2 cos ⁡ t + 2 cos ⁡ t + 2 t   s e n   t - cos ⁡ t 0 2 π

Aplicando os limites de integração, ficamos com:

z - = 1 8 π 3 3 + 2 π - ( 2 π ) 2 cos ⁡ 2 π + 2 cos ⁡ 2 π + 2 ( 2 π )   s e n   2 π - cos ⁡ 2 π - ( 2 cos ⁡ 0 - cos ⁡ 0 )

Resolvendo, temos que:

z - = 1 8 π 3 3 + 2 π - 4 π 2 + 2 + 0 - 1 - ( 2 - 1 )

Simplificando, temos que:

z - = - 4 π 2 8 π 3 3 + 2 π

Organizando um pouco melhor a expressão, vamos ter:

z - = - 6 π 4 π 2 + 3

Resposta

m = 2 8 π 3 3 + 2 π

6 π 3 + 3 π 4 π 2 + 3 ,   6 4 π 2 + 3 ,   - 6 π 4 π 2 + 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Escreva fórmulas semelhantes à Equação 4 para o centro de massa x C M ,y C M ,z C M de um arame fino com função densidade ρ x ,y ,z e forma da curva espacial C .(b) Determine o centro de massa de
Se um arame com densidade linear ρ x ,y está sobre uma curva plana C , seus momentos de inércia em relação aos eixos x e y são definidos por I x = ∫ C y 2ρ x ,y d s I y = ∫ C x 2ρ x ,y d s Determine o
Se um arame com densidade linear ρ x ,y ,z está sobre uma curva espacial C , seus momentos de inércia em relação aos eixos x , y e z são definidos por I x = ∫ C ( y 2 + z 2 ) ρ x ,y d s I y = ∫ C ( x
Se F é o campo vetorial do Exemplo 5, mostre que ∫ C F ⋅ d r = 0 para todo caminho fechado simples que não passe pela origem e nem a circunde. F x , y = - yi + xj x 2 + y 2
Use o Exercício 22 para encontrar o centroide de um quarto de uma região circular de raio a .