Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 32
(a) Determine o trabalho realizado pelo campo de força sobre uma partícula que dá uma volta no círculo no sentido anti-horário.
(b) Utilize um sistema de computação algébrica para desenhar o campo de força e o círculo na mesma tela. Use essa figura para explicar sua resposta para a parte (a).
Passo 1
Fala, meu povo! Tudo certo?
Nossa questão tem duas partes, vamos ver cada uma separadamente:
A parte a) pede o trabalho realizado pelo campo de força
numa partícula que dá a volta no círculo no sentido anti-horário.
Bom, nós achamos o trabalho calculando a integral de linha:
Então, como nossa curva é o círculo , precisamos parametrizar essa nossa região em função de . Daí é só derivarmos o vetor das nossas funções paramétricas para obter e colocarmos nossa função nas variáveis paramétricas para acharmos . Daí é só calcularmos nossa integral normalmente.
Depois faremos a letra b) que pede para usarmos um sistema de computação algébrica para desenhar o campo de força e o círculo e através dessa imagem explicar a resposta da parte a). Podemos usar o software Maple para plotar o gráfico.
Vem comigo!
Passo 2
- Galera, quando temos um círculo, podemos parametrizar de uma forma análoga ao que fazíamos com as coordenadas polares:
- Agora vamos usar um SCA para desenhar o campo de força junto com o círculo. Podemos usar o software Maple usando a função fieldplot e inserindo a equação da função do campo e as equações paramétricas do círculo:
é o raio do círculo. Como nossa equação é:
E a equação de um raio do círculo é:
Podemos ver que:
Então, nossas equações paramétricas para o círculo serão:
Ou seja:
Passo 3
A derivada de cada componente desse vetor será:
E nossa função:
Parametrizada, ou seja, substituindo e pelas equações em função de , fica:
Então teremos:
Fazendo o produto vetorial, temos que o trabalho vai ser calculado assim:
Passo 4
Agora que já definimos nossa integral, é só partir para o cálculo:
Reparou que os termos dentro da integral são opostos? Então, fazendo a subtração, ficamos com zero!
Já que a integral de zero é zero!
Passo 5
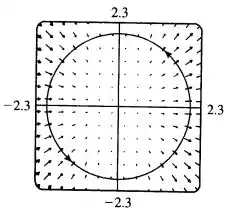
Parece que todas as setas dos vetores são perpendiculares ao círculo. Sabe o que isso significa? As forças exercidas sobre a partícula não ajudam nem atrapalham o movimento dela ao longo do círculo, e por isso o trabalho é nulo, como calculamos anteriormente.