Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 17
Dê o domínio e esboce o gráfico de
Passo 1
Antes de tudo, vamos dar uma espiadinha na questão anterior.
Lá verificamos que:
E chegamos a seguinte conclusão: à medida que vai se tornando cada vez maior, o denominador da fração vai se tornando cada vez maior, e a fração vai se tornando cada vez mais próxima de zero.
Ou seja, à medida que cresce, a diferença vai se aproximando cada vez mais de zero!
Como , isso significa que à medida que cresce, o gráfico de vai encostando por cima do gráfico de .
Passo 2
Então, fazendo o mesmo raciocício, temos que:
E daí vamos refazer a análise: à medida que cresce, o gráfico vai encostando por baixo no gráfico de .
E o domínio? Bom, temos que para raiz de índice par, o radicando não pode ser negativo, então:
Isso nos dá que ou . E o domínio de pode ser escrito dessa forma:
Passo 3
Vamos ao esboço do gráfico? As raízes da função são onde , então:
Os pontos onde a função corta o eixo dos é e . Usando um programa de geração gráfica temos:
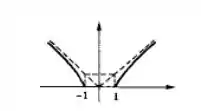
Resposta
