Sua empresa decidiu lançar uma versão de luxo da frigideira que você projetou. O plano é esmaltá-la de branco por dentro e de azul por fora. A camada de esmalte terá de espessura antes de ir ao forno. (Veja o diagrama a seguir). O departamento de produção quer saber a quantidade de esmalte que precisará dispor para produzir frigideiras. O que você diria a eles? (Ignore o desperdício e a matéria-prima não utilizada; dê a sua resposta em litros. Lembre-se de que logo .)

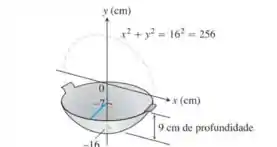
Para resolver essa questão precisamos calcular a área da superfície da frigideira. A imagem nos fornece a função que devemos utilizar e nos mostra o eixo de rotação que é o eixo , assim como os limites de integração. Assim, por definição para calcular a área de uma superfície rotacionada sobre o eixo por uma função, temos:

Isolando nossa função:

Observe que como queremos calcular a área, desconsideramos a parte negativa.

Logo: