Exercícios de Área de Superfícies de Revolução - Lista de Exercícios Resolvida
Questão 1
Determine a área de superfície gerada pela rotação, em torno do eixo , do pedaço de astróide , mostrado a seguir
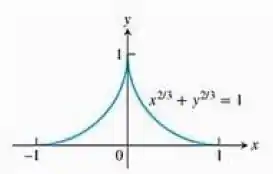
Dica: Gire o pedaço do primeiro quadrante em torno do eixo e dobre o resultado
Ver solução completaQuestão 2
a) A fórmula da área de superfície foi desenvolvida sob o pressuposto de que a função , cujo gráfico gerou a superfície, era não negativa no intervalo de integração. Para curvas que cruzam o eixo de revolução, substituímos a equação pela fórmula de valor absoluto
Use essa equação para determina a área de superfície do cone duplo gerado pela rotação, em torno do eixo , do segmento de reta ,
b) Determine a área de superfície gerada pela rotação, em torno do eixo , da curva
Ver solução completaQuestão 3
Determine as áreas das superfícies geradas pela rotação da curvas em torno dos eixos indicados.
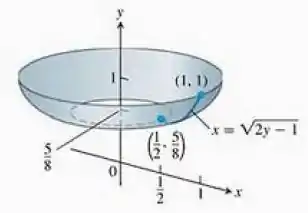
Questão 4
Eis um desenho esquemático da redoma de pés usada pelo Serviço Meteorológico Nacional dos Estados Unidos para abrigar um radar em Bozeman, Montana.
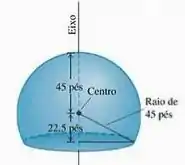
Se a redoma fosse pintada, qual a área da superfície que receberia tinta (sem contar a base)?
Ver solução completaQuestão 5
Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do eixo indicado
Com
Rotacionando em torno do eixo
Ver solução completaQuestão 6
17 - Determine a área da superfície lateral do cone gerado pela rotação, em torno do eixo , do segmento de reta , com .
Ver solução completaQuestão 7
18 - Determine a área da superfície lateral do cone gerado pela rotação, em torno do eixo , do segmento de reta , com .
Ver solução completaQuestão 8
21 - Determine a área das superfícies geradas pela rotação das curvas em torno do eixo indicado:
c) , com , eixo .
Ver solução completaQuestão 9
21 - Determine a área das superfícies geradas pela rotação das curvas em torno do eixo indicado:
a) , com , eixo .
Ver solução completaQuestão 10
19 - Determine a área da superfície de cone gerado pela rotação, em torno do eixo , do segmento de reta , com .
Ver solução completaQuestão 11
21 - Determine a área das superfícies geradas pela rotação das curvas em torno do eixo indicado:
b) , com , eixo .
Ver solução completaQuestão 13
Mostre que a área de um elipsóide de revolução obtido rotacionando a elipse
em torno do eixo é dada por:
Ver solução completaQuestão 14
Quando giramos o gráfico de uma função de classe , , , em torno do eixo , obtemos uma superfície de revolução, cuja área é definida pela integral
(para maiores detalhes, veja o livro do Stewart vol. , seção )
Calcule a área da superfície de revolução obtida pela rotação em torno do gráfico de cada função indicada. Faça um esboço da superfície.
Ver solução completa
Questão 16
Quando giramos o gráfico de uma função de classe , , , em torno do eixo , obtemos uma superfície de revolução, cuja área é definida pela integral
(para maiores detalhes, veja o livro do Stewart vol. , seção )
Calcule a área da superfície de revolução obtida pela rotação em torno do gráfico de cada função indicada. Faça um esboço da superfície.
Ver solução completa
Questão 17
Determine a área das superfícies geradas pela rotação das curvas em torno do eixo indicado:
e) , com , eixo
Ver solução completaQuestão 18
Determine a área das superfícies geradas pela rotação das curvas em torno do eixo indicado:
d) , com , eixo
Ver solução completaQuestão 19
A região sob o gráfico de no intervalo é girado em torno do eixo . Encontre o volume do sólido gerado.
Ver solução completaQuestão 21
Desenhe o conjunto abaixo e calcule a área:
d) é o conjunto de todos tais que .
Ver solução completaQuestão 22
Desenhe o conjunto abaixo e calcule a área:
p) é o conjunto de todos os pontos tais que e .
Ver solução completaQuestão 23
Desenhe o conjunto abaixo e calcule a área:
n) é o conjunto de todos os pontos tais que .
Ver solução completaQuestão 24
Desenhe o conjunto abaixo e calcule a área:
o) é o conjunto de todos os pontos tais que .
Ver solução completaQuestão 25
Desenhe o conjunto abaixo e calcule a área:
g) é o conjunto do plano limitado pela reta e pelo gráfico de , com .
Ver solução completaQuestão 26
Determine a área das superfícies geradas pela rotação das curvas em torno do eixo indicado:
f) com , eixo
Ver solução completaQuestão 27
Desenhe o conjunto abaixo e calcule a área:
b) é o conjunto do plano limitado pelas retas , , e pelo gráfico .
Ver solução completaQuestão 28
Determine a área da superfície de revolução gerada pela rotação das curvas:
em torno do eixo .
Ver solução completaQuestão 29
Determine a área da superfície de revolução gerada pela rotação das curvas:
em torno do eixo .
Ver solução completaQuestão 30
Determine a integral que representa o volume do elipsóide gerado pela rotação da curva , em torno do eixo .
Ver solução completaQuestão 31
Determine a área da superfície de revolução gerada pela rotação das curvas:
em torno do eixo .
Ver solução completaQuestão 32
Determine a área da superfície de revolução gerada pela rotação das curvas:
em torno do eixo .
Ver solução completaQuestão 33
Desenhe o conjunto abaixo e calcule a área:
m) é o conjunto do plano limitado pelas retas , e pelos gráficos de e .
Ver solução completaQuestão 34
Desenhe o conjunto abaixo e calcule a área:
f) é a região do plano compreendida entre o eixo e o gráfico de , com .
Ver solução completaQuestão 35
Dadas as superfícies e de equações e , respectivamente, obtenha uma parametrização da curva formada pela interseção de com e que está localizada acima do plano .
Ver solução completaQuestão 36
Desenhe o conjunto abaixo e calcule a área:
k) é o conjunto do plano limitado pela reta , pelo gráfico , com .
Ver solução completaQuestão 37
Desenhe o conjunto abaixo e calcule a área:
h) é o conjunto do plano limitado pelas retas , e pelo gráfico de .
Ver solução completaQuestão 38
Desenhe o conjunto abaixo e calcule a área:
c) é o conjunto de todos tais que .
Ver solução completaQuestão 39
Desenhe o conjunto abaixo e calcule a área:
i) é o conjunto do plano limitado pelas retas e pelo gráfico de
Ver solução completaQuestão 40
Desenhe o conjunto abaixo e calcule a área:
a) é o conjunto do plano limitado pelas retas pelo eixo e pelo gráfico .
Ver solução completaQuestão 41
Desenhe o conjunto abaixo e calcule a área:
e) é o conjunto de todos tais que , com .
Ver solução completaQuestão 42
Determine a área da superfície de revolução gerada pela rotação das curvas:
em torno do eixo .
Ver solução completaQuestão 43
Determine a área da superfície de revolução gerada pela rotação das curvas:
em torno do eixo .
Ver solução completa