Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 12

Encontrando a massa: encontre a massa de uma placa fina ocupando a região menor cortada pela elipse x 2 + 4 y 2 = 12 pela parábola x = 4 y 2 se δ x , y = 5 x

Passo 1

Faaaala, cara! Tranquileba?

Olhando o gráfico fica mais fácil pra gente perceber os limites:

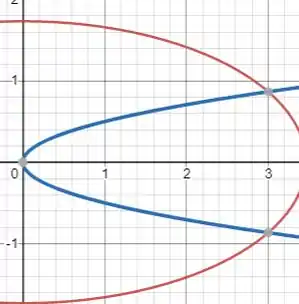
Temos que o eixo c é limitado de - 3 2 . 3 2 e o eixo x de 4 y 2 ,   12 - 4 y 2

Sabendo que é massa é definida por:

M = ∬ δ x , y d x d y

Já temos informação necessário para chegarmos ao resultado

Passo 2

Assim sendo, temos que:

M = ∫ - 3 2 3 2 ∫ 4 y 2 12 - 4 y 2 5 x d x d y

= ∫ - 3 2 3 2 5 ∫ 4 y 2 12 - 4 y 2 x d x d y

∫ - 3 2 3 2 5 x 2 2 4 y 2 12 - 4 y 2 d y

Passo 3

5 2 ∫ - 3 2 3 2 12 - 4 y 2 - 16 x 4 d y

= 5 2 12 y - 4 3 y 3 - 16 5 y 5 - 3 2 3 2

M = 23 3

Resposta

M = 23 3

Exercícios de Livros Relacionados

Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é o cubo dado por 0 ≤ x ≤ a , 0 ≤ y ≤ a , 0 ≤ z ≤ a ; ρ x , y , z = x 2 + y 2 + z 2
Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é o tetraedro limitado pelos planos x = 0 ,y = 0 ,z = 0 ,x + y + z = 1 ρ x , y , z = y
Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é limitado pelo cilindro parabolóico z = 1 - y 2 e pelos planos x + z = 1 , x = 0 e z = 0 ; ρ x , y , z = 4
Utilize coordenadas cilíndricas.Determine a massa da bola B dada por x 2 + y 2 + z 2 ≤ a 2 se a densidade em qualquer ponto for proporcional à sua distância do eixo z .
Utilize coordenadas cilíndricas.Determine a massa e o centro de massa do sólido S delimitado pelo paraboloide z = 4 x 2 + 4 y 2 e pelo plano z = a( a0 ) , se S tem densidade constante K .