Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 37

Encontre del z // del u e del z // del v quando u = ln 2 , v = 1 se z = 5 tg^(- 1) x e x = e^u + ln v .

Passo 1

Oi galerinha, para encontrarmos del z // del u e del z // del v , vamos primeiro fazer o diagrama de árvore, para montarmos a equação da regra da cadeia. Então:

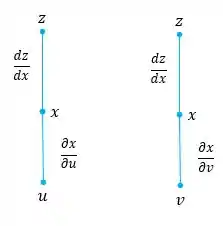
Onde:

Agora iremos calcular as derivadas del x // del u e del x // del v , e sabemos que {[[u = ln 2],[v = 1]]) .

Temos que x = e^u + ln v , logo:

(del x)/(del u) = e^u = e^((ln 2))

(del x)/(del u) = 2

E:

(del x)/(del v) = (1)/(v) = (1)/(1)

(del x)/(del v) = 1

Passo 2

Para calcularmos a derivada d z // d x , vamos substituir os valores de {[[u = ln 2],[v = 1]]) na equação de x :

x = e^((ln 2)) + ln 1 = 2 + 0

x = 2

Agora vamos encontrar a derivada da função:

z = 5 tg^(- 1) x

Sabemos que:

y = tg^(- 1) u -> y^' = (1)/(1 + u^2)

Logo:

(d z)/(d x) = 5 * (1)/(1 + x^2) = (5)/(1 + x^2)

= (5)/(1 + 2^2) = (5)/(5)

(d z)/(d x) = 1

Passo 3

Substituindo os valores encontrados:

(del z)/(del u) = 1 * 2 = 2

(del z)/(del v) = 1 * 1 = 1

Tchau! Até mais.

Resposta

(del z)/(del u) = 2 , (del z)/(del v) = 1 .

Exercícios de Livros Relacionados

Suponha que z = z ( x , y ) satisfaça a equação x 2 ∂ 2 z x , y ∂ x 2 + 2 x y ∂ 2 z x , y ∂ x ∂ y - x ∂ z x , y ∂ x = x 3 y 2 . Fazendo a mudança de variáveis x = e u , y = e v . Calcule ∂ 2 z x , y ∂
Verifique que a mudança de variáveis x = s c o s θ - t s e n ( θ ) , y = s sen ⁡ θ + t c o s ( θ ) com θ constante , transforma a equação ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 ( u = u ( x , y ) ) Em ∂ 2 u ∂ s
Verifique que a mudança de variáveis u = x + y , v = y + 2 x transforma a equação ∂ 2 z u , v ∂ x 2 - 3 ∂ 2 z x , y ∂ x ∂ y + 2 ∂ 2 z x , y ∂ y 2 = 0 Em, ∂ 2 z u , v ∂ u ∂ v = 0
a) Ache uma função u ( x , y ) da forma u x , y = F x 2 + y 2 que satisfaça a equação de Laplace ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 b) Faça a mesma coisa para funções de três ou mais variáveis.
Sejam G (u , v) = (F (x , y))/(x) , u = x + y e v = (y)/(x) . Suponha que (del^2 F)/(del x^2) - 2 (del^2 F)/(del x del y) + (del^2 F)/(del y^2) = 0 . Calcule (del^2 G)/(del v^2) .