Encontre a área da região delimitada pelas curvas dadas
Passo 1
Pra facilitar a visualização, podemos esboçar um gráfico das duas funções )
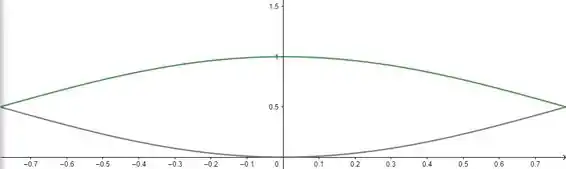
Então, podemos ver que a área delimitada pelas curvas pode ser escrita como uma função tal que
Passo 2
Agora, podemos encontrar a área da região delimitada pela função (pelas duas curvas) tomando a integral no intervalo dado
Para resolver esta integral, precisamos lembrar da seguinte propriedade trigonométrica:
Então, podemos substituir
Agora, resolvendo pelo método da substituição
Seja , temos que . Vamos calcular também os novos limites de intergração