Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 54
- Encontre as assíntotas verticais e horizontais.
- Encontre os intervalos nos quais a função é crescente ou decrescente.
- Encontre os valores máximos e mínimos locais.
- Encontre os intervalos de concavidade e os pontos de inflexão.
- Use a informação das partes (a) – (d) pra esboçar o gráfico de .
Passo 1
E aí! tudo certinho?
Nesse problema foi dada a função
E ela nos pede uma série de coisas... as assíntotas horizontais e verticais, os intervalos crescente e decrescente da função, os valores máximos e mínimos locais, os intervalos de concavidades, os pontos de inflexão e ainda temos que esboçar o gráfico de
Bastante coisa, não é?
As assíntotas horizontais são obtidas em , onde é obtido em
As assíntotas horizontais são obtidas como , onde é obtido a partir de
Os intervalos de crescimento e decrescimento são obtidos a partir da derivada de onde em obtemos o intervalo de crescimento e o intervalo de decrescimento.
Para obter os máximos e mínimos locais, fazemos para obter os pontos críticos e aplicamos o teste da segunda derivada... esse teste consiste em calcular a segunda derivada de e aplicar os pontos críticos... , é um ponto de mínimo, mas se , é um ponto de máximo.
Os pontos de inflexão são obtidos quando e as concavidades são determinadas quando (concavidade positiva) e (concavidade negativa).
Bora começar!
Passo 2
No item a) precisamos achar as assíntotas, então vamos calcular os limites.
Primeiro, vamos achar assíntota horizontal,
Como só é definida para , para não temos limite.
Como o limite não tendeu a um valor, não temos nenhuma assíntota horizontal.
Já vertical, como a função é contínua em todo seu domínio , podemos imaginar que em podemos ter uma assíntota vertical.
Assim, é assíntota vertical.
Tranquilo até aqui?
Passo 3
No item b) precisamos achar onde cresce ou decresce, mas pra isso precisamos da derivada e dos pontos críticos, então vamos encontrá-los.
Derivando , usando a regra da potência, temos que
Organizando o resultado...
No passo 1 vimos que se a função é crescente, ou seja
Podemos perceber que essa inequação é válida para , então nesse intervalo a função é crescente.
Agora para , a função é decrescente e isso acontece em
Ou seja, quando e e função é decrescente...
Show?
Passo 4
Precisamos achar nossos candidatos a máximo e mínimo, ou seja, pontos críticos. Esses pontos são obtidos quando , ou seja...
Então os pontos críticos são e .
No passo anterior vimos que é decrescente até e depois desse ponto ele cresce, portanto é um ponto de mínimo local e vale
A função cresce em até e a partir daí ela decresce, então é um ponto de máximo local e vale
Bacana, não é?
Passo 5
Precisamos saber da concavidade da função, beleza?
Então vamos calcular a segunda derivada e analisar seu sinal...
Usando a regra do quociente, temos que
Perceba que podemos simplificar alguns termos do numerador...
O sinal de está diretamente ligada à concavidade do gráfico da função, então se , temos
Então para a função possui concavidade para cima.
Já quando , temos
Ou seja, para a concavidade é voltada para baixo.
Maravilha!
Passo 6
Os pontos de inflexão da função são determinados quando , logo
Então é nosso ponto de inflexão e isso faz sentido pois nesse ponto a função muda de concavidade!
Estamos quase no fim!
Passo 7
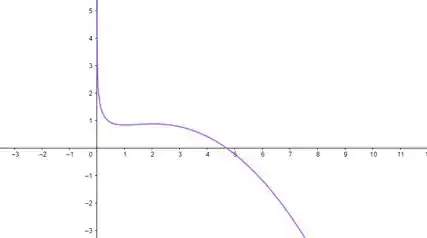
Agora, temos que esboçar o gráfico a partir das informações que obtemos anteriormente.
Vimos que em temos um ponto de mínimo e em temos um ponto de máximo.
A função é decrescente em e em e crescente em .
Temos um ponto de inflexão em .
A concavidade do gráfico é voltada para cima em e para baixo em .
Com isso podemos esboçar o gráfico de como:
Resposta
è decrescente em e . Além disso, possui concavidade para cima em e para baixo , sendo o ponto de inflexão.
