Encontre o domínio e esboce o gráfico da função:
Passo 1
E aí! tudo certinho? 😉

Nesse problema foi dada a função
E nosso objetivo é determinar o domínio e esboçar o gráfico dessa função. Para encontrar o domínio, deveremos pensar em quais valores de nossa função pode aceitar. Se existe alguma restrição para algum valor.
O gráfico, a gente precisa entender o comportamento da função para valores negativos que entram no mudo e para valores positivos. Veja que a função modulo é assim:
Então se a gente prestar atenção que temos duas equações em cada intervalo, a gente consegue gerar esse gráfico tranquilamente.
Parece complicado? 😉
Passo 2
Bom galera, para trabalhar com esse tipo de questão, temos que saber trabalhar com a função módulo:
Primeiro de tudo, a função módulo não tem nenhum tipo de restrição com relação ao seu domínio. Como temos um polinômio de primeiro grau dentro de um módulo, podemos afirmar tranquilamente que o domínio da função é o conjunto de todos os números reais .
Ou seja, o domínio da função é igual à .
O domínio de uma função pode ser definido como os possíveis valores que a variável da função pode assumir para a função ser definida.
Veja só! 😬
Passo 3
A função módulo pode ser enxergada como se fosse um “resumo” de duas outras funções (uma positiva e uma negativa). Olha como a gente pode escrever isso:
Viu como temos duas sentenças agora? Cada uma vai dizer o comportamento de parte da função de acordo com a regra quem tem do lado. A gente vai ter que ajeitar essas regras, fazendo com que elas fiquem em função de :
Agora, a gente só vai ajeitar o sinal negativo da segunda expressão que a gente tem, ficando:
Pronto! Essa nossa expressão final é a nossa função módulo escrita direitinho como a gente precisa para desenhar o gráfico dela!
Tranquilo até aqui! 👀
Passo 4
Bom, de acordo com a sentença que a gente achou, a nossa função, quando , vai se comportar como uma reta crescente cuja expressão é .
Quando tivermos na nossa função, aí vamos ter o comportamento de uma reta decrescente cuja expressão é . Sacou? Da uma olhada em como vai ficar o nosso gráfico:
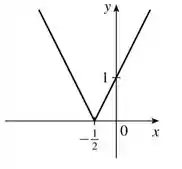
Pronto! Essa questão já foi! ;)
E aí! entendeu tudo? Responde Aí! 😉
Resposta
Para o domínio da função, temos que . O gráfico da função ficará da seguinte forma: