Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.3 - Ex. 9
- Encontre os intervalos nos quais é crescente ou decrescente.
- Encontre os valores máximo e mínimo locais de.
- Encontre os intervalos de concavidade e os pontos de inflexão.
Passo 1
Faaala meus lindões.
Nessa questão nos é dado a seguinte função:
E para ela queremos encontrar os intervalos que é crescente e os intervalos em que é decrescente.
Para isso, vamos derivar a função
e então encontrar os intervalos em que a derivada é positiva (função crescente) e os intervalos em que a derivada é negativa (função decrescente).
Depois, vamos encontrar os pontos de máximo e mínimo locais.Para isso, vamos encontrar os pontos em que a derivada é zero.
E fazendo a análise do crescimento e decrescimento podemos avaliar se esses pontos são de máximo ou mínimo.
Por fim, vamos encontrar os intervalos de concavidade e pontos de inflexão.Para isso vamos encontrar a segunda derivada da função
E os intervalos onde a segunda derivada é positiva, temos concavidade para cima. Os intervalos que a segunda derivada énegativa, temos concavidade para baixo. E por fim, os pontos onde a segunda derivada vale zero são os pontos de inflexão.Bora lá!
Passo 2
Para a letra a) queremos encontrar os intervalos decrescimento e decrescimento
Nossa função é:
Derivando uma vez, temos:
Para analisar o sinal da derivada, vamos encontrar onde ela é zero.
Bom, agora vamos ver como essa derivada se comporta para valores menores que , entre e e maiores que .
Vou usar aqui os valores e .
Portanto a derivada é positiva para valores menores que .
Ela é negativa para valores entre e .
E ela é positiva para valores maiores que .
Portanto, nosso estudo de sinais resultou em:
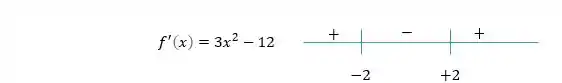
Portanto, a função é crescente para valores menores que , é decrescente entre e e é crescente para valores maiores que .
Passo 3
Na letra b) queremos os máximos e mínimos locais.Vemos pela derivada que ela vale zero em:
Portanto, esses são os nossos pontos críticos.
Olhando o estudo de sinais da derivada vemos que:
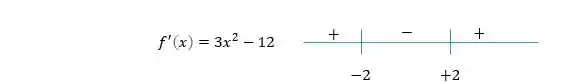
Como no ponto , a função antes era crescente e depois se tornou decrescente, temos que esse ponto é um ponto de máximo local.
Já no ponto ,a função antes era decrescente e depois se tornou crescente, portanto esse ponto é um ponto de mínimo local.
Máximo local:
Mínimo local:
Passo 4
Agora para verificar os pontos de inflexão e analisar a concavidade, vamos avaliar a derivada segunda!
Essa derivada segunda zera em:
Então temos apenas um ponto de inflexão: .
Antes dele vemos que a concavidade da função é negativa (concavidade para baixo)
E depois é positiva (concavidade para cima)
E é isso! Espero ter ajudado!
Resposta
- crescente nos intervalos:
- é máximo local e é um valor de mínimo local.
- sabemos que é côncava para baixo em e côncava para cima em , e há um ponto de inflexão em .
E decrescente quando: