(a) Encontre os intervalos crescentes e decrescentes.
(b) Encontre os valores do máximo e mínimo.
(c) Encontre os intervalos de concavidade e os pontos de inflexão.
(d) Use a informação das partes (a)-(c) para esboçar um gráfico. Confira seu esboço com um gráfico de software.
Passo 1
E aí! como vai?
Nesse problema foi dada a função
e nosso objetivo é encontrar os intervalos onde a função é crescente e decrescente, os valores de máximos e mínimos, os intervalos de concavidade, os pontos de inflexão e esboçar o gráfico da função a partir das informações que obtemos.
Bastante coisa, não é?
Para encontrar os intervalos de crescimento e decrescimento da função, vamos calcular sua derivada e como a inclinação da função está relacionada diretamente com sua derivada:
- Quando a função é crescente e quando a função é decrescente.
- Se , o ponto é de mínimo e se , o ponto é de máximo.
- Quando a concavidade é para cima e quando a concavidade é para baixo.
Para calcular os máximos e mínimo vamos calcular os pontos críticos fazendo e a partir da análise dos intervalos de crescimento e decrescimento podemos dizer qual é máximo e qual é mínimo ou podemos usar o teste da segunda derivada...
Os intervalos de concavidade são obtidos pela segunda derivada da função...
Já os pontos de inflexão são obtidos onde .
Bora começar!
Passo 2
Então vamos começar derivando a função pela regra da potência
Fatorando este resultado vamos poder analisar o sinal de maneira mais fácil...
Fazendo para encontrar os pontos críticos, temos que , e são os pontos que zeram essa função, logo esses são os pontos críticos...
Agora vamos analisar quando vão ocorrer mudanças de sinal. Uma dica é prestar atenção nos intervalos entre os pontos críticos.
Para , temos que , e , então
Para , temos que , e , ou seja
E para , temos que , e , dessa forma
E por fim, para , temos que , e , logo
Portanto, se a função é crescente e a função é decrescente, então
é crescente para em e .
é decrescente para em e .
Show?
Passo 3
Para encontrar os valores de máximos e mínimos da função, vamos então encontrar a segunda derivada, derivando
Fatorando o resultado:
Da letra (a), temos que nos pontos , e
Vamos utilizar estes pontos críticos em e ver o sinal:
Para
Assim, como , o ponto é um ponto de máximo.
Para
Logo, como , é um ponto de m��nimo.
E por último, para
Então tambem é um ponto de mínimo.
Agora vamos voltar para a função para ver os valores associados:
Tranquilo até aqui?
Passo 4
Para descobrir a concavidade, temos que olhar para os intervalos da segunda derivada...
Vamos fazer a mesma análise que fizemos no passo 2...
Então checando nos intervalos próximos das raízes:
Para , o termo e , então
E, portanto, nesse intervalo a concavidade é voltada para cima...
Para , o termo e , então
Assim, nesse intervalo a função tem uma concavidade voltada para baixo
E para , o termo e , com isso
Portanto, nesse intervalo possui outra concavidade voltada para cima.
Estamos quase no fim!
Passo 5
Os pontos de inflexão ocorrem quando , ou seja
Para essa igualdade ser satisfeita, tem que ser ou pois nesses pontos e zeram respectivamente.
Está acompanhando?
Passo 6
Agora temos que condensar tudo que encontramos até aqui para esboçar o gráfico de .
Bom... possui um ponto de máximo local em e dois pontos de mínimos locais em .
Além disso, nos intervalos e a função possui concavidade voltada para cima e no intervalo a concavidade é voltada para baixo.
A função possui dois pontos de inflexão, um em e outro em , que é onde a função muda de concavidade.
Traçando o gráfico da função, temos:
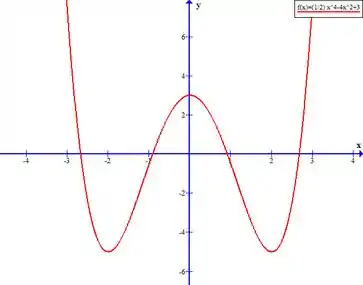
E fim! O que achou? Responde Aí!
Resposta
(a)
(b)
(c)