Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 43
- Encontre os intervalos em que a função é crescente ou decrescente.
- Encontre os valores máximo e mínimo locais.
- Encontre os intervalos de concavidade e pontos de inflexão.
- Use as informações de a) - c) para esboçar o gráfico.
Verifique seu trabalho com uma ferramenta gráfica, se você tiver uma.
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente a função
E teremos que dizer algumas coisas sobre ela.
No item (a) precisamos encontrar os intervalos nos quais a função é crescente ou decrescente.
Para saber isso podemos usar as informações dadas pela derivada da função, pois ela representa a inclinação da reta tangente ao gráfico da função. Assim, se
Significa que a função é crescente, já que a reta tangente tem derivada positiva. E se
A função é decrescente, j�� que a derivada é negativa.
No item (b), queremos encontrar os valores de máximo e mínimo locais.
Para isso também usamos a ideia dada pela inclinação da reta tangente. Ou seja, a derivada. Assim:
Teremos um ponto de máximo ou mínimo da função, já que a inclinação da reta tangente será nula.
No item (c) vamos encontrar os intervalos de concavidade e os pontos de inflexão.
E aqui faremos uso da derivada segunda. Sabendo que se:
Nossa curva terá concavidade para baixo.
E se
E nossa curva terá concavidade para cima.
E finalmente, no item (d) vamos usar as informações das partes (a)-(c) para esboçar o gráfico de .
Agora que já sabemos o que fazer em cada item, vem comigo que te mostro como vai ficar tudo isso.
Passo 2
Vamos resolver por ordem dos itens, beleza?
No item a) precisamos achar onde cresce ou decresce, mas pra isso precisamos da derivada e dos pontos críticos, então vamos encontra-los.
Derivando , usando a regra do produto, temos que:
Organizando as contas:
Precisamos achar nossos candidatos a máximo e mínimo, ou seja, pontos críticos. Já temos o primeiro, pois torna indefinida.
Agora, vamos encontrar o resto, fazendo:
Ou seja:
Como o denominador não pode zerar, precisamos que:
Isolando , temos:
Esse é o nosso segundo ponto crítico.
Passo 3
Agora, precisamos analisar as proximidades desse ponto para usar o teste da primeira derivada e obter os valores de máximos e mínimos.
Temos que:
se
se
(você pode verificar isso pegando números no intervalo que te dei e aplicando na derivada).
Assim, pelo teste da primeira derivada, é crescente em e decrescente no intervalo .
Passo 4
Para responder ao item b), vamos usar o item anterior, olha só!
Repare que em , a nossa função deixou de ser crescente e passou a ser decrescente. Isso indica que representa um máximo local da função. Além disso, também conseguimos inferir da análise de sinal no passo anterior, que não existe ponto de mínimo local para essa função.
Uma outra forma de verificar isso seria calculando a segunda derivada da função e substituindo o ponto no resultado, de forma que encontraríamos , indicando também o ponto de máximo.
Passo 5
Agora precisamos analisar a concavidade da função, beleza? Então, vamos calcular a segunda derivada.
Usando a regra do quociente, temos que:
Arrumando as contas:
Perceba que nosso primeiro candidato a ponto de inflexão é pois nele a é indefinida. Vamos achar o resto agora, fazendo:
Ou seja:
Desse modo, temos:
Isolando :
Mas para , nossa função também não está definida, pois teríamos a raiz quadrada de um número negativo. Então, vamos considerar apenas na análise.
Passo 6
Vamos verificar o que acontece nas proximidades do ponto que encontramos no passo anterior, para verificar se ele é mesmo um ponto de inflexão. Vamos lá!
Perceba que:
se
(você pode verificar isso pegando números menores que 6 e aplicando na derivada).
O que significa que é côncava para cima nesse intervalo. Então não temos um ponto de inflex��o.
Passo 7
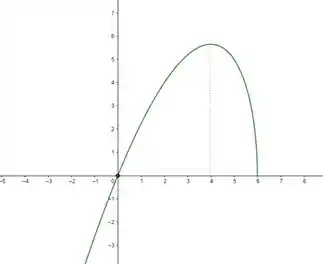Só falta esboçar o gráfico. Partiu!
Prontinho, galera! Até a próxima! 😉