Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 35
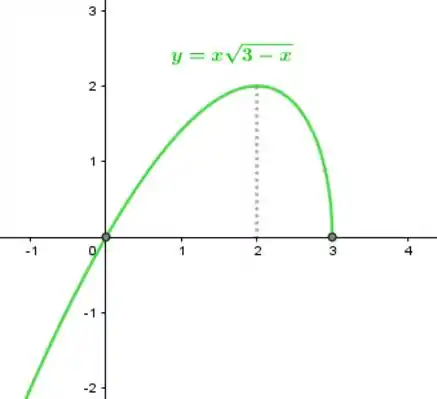
Faça o gráfico da curva
Passo 1
Inicialmente vamos considerar e observar o que essa função tem a nos “dizer”.
Observe que o domínio de corresponde , pois qualquer valor maior que esse ocasionaria em uma raiz quadrada negativa, que é algo que não existe no conjunto dos números Reais .
Sendo assim, o gráfico de a partir de não assume valor algum. Isso acontece pois a função não está definida para esses valores.
Passo 2
Em seguida verificaremos, se possui raízes, ou seja, se o gráfico toca o eixo
Com isso percebemos que para e temos que ou seja,
E,
Logo, o gráfico de toca o eixo duas vezes.
Passo 3
Determinaremos agora e , para em seguida verificarmos se possui máximos, mínimos ou pontos de inflexão. Dessa maneira temos que,
Utilizando o fato de e pela regra da produto teremos,
Calculando a segunda derivada utilizando a regra da soma e a regra do produto
Passo 4
Vamos agora identificar se possui pontos críticos
Em relação aos pontos de críticos temos que
Sendo assim temos um candidato à ponto crítico, vamos verificar se qual a mudança de sinal nas proximidades dele.
Perceba que, para valores dentro do intervalo , assume valores positivos (crescente). E para valores dentro do intervalo , irá assumir valores negativos (decrescente). Logo, é um ponto de máximo no intervalo de
Passo 5
Vamos agora identificar se possui pontos de inflexão
Em relação aos pontos de inflexão temos que
Sendo assim temos um candidato a ponto de inflexão, vamos verificar se há mudança de sinal nas proximidades dele.
Perceba que , para valores dentro do intervalo , assume valores negaitivos (Concavidade para baixo ). E para valores dentro do intervalo , irá assumir valores negativos (Concavidade para baixo). Logo, não é um ponto de inflexão no intervalo de
Sendo assim, não é um ponto de inflexão para ,ou seja, não há mudança de concavidade.
Passo 6
Para finalizar verificaremos se possui assíntotas verticais ou horizontais.
No que se refere as assíntotas horizontais temos que
No que se refere as assíntotas horizontais temos que
Sendo que pois o domínio de está definido para .
Portanto, não possui assíntotas horizontais.
No que se refere as assíntotas verticais, não há nenhum ponto no domínio de que faça com que
Logo, não possui assíntotas verticais.
Resposta
