Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 42
(a) Encontre os intervalos em que a função é crescente ou decrescente.
(b) Encontre os valores máximos ou mínimos locais.
(c) Encontre os intervalos de concavidade e os pontos de inflexão.
(d) Use as informações das partes (a)-(c) para esboçar o gráfico. Verifique seu trabalho com uma ferramenta gráfica, se você tiver uma.
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente a função
E teremos que dizer algumas coisas sobre ela.
No item (a) precisamos encontrar os intervalos nos quais a função é crescente ou decrescente.
Para saber isso podemos usar as informações dadas pela derivada da função, pois ela representa a inclinação da reta tangente ao gráfico da fun��ão. Assim, se
Significa que a função é crescente, já que a reta tangente tem derivada positiva. E se
A função é decrescente, já que a derivada é negativa.
No item (b), queremos encontrar os valores de máximo e mínimo locais.
Para isso também usamos a ideia dada pela inclinação da reta tangente. Ou seja, a derivada. Assim:
Teremos um ponto de máximo ou mínimo da função, já que a inclinação da reta tangente será nula.
No item (c) vamos encontrar os intervalos de concavidade e os pontos de inflexão.
E aqui faremos uso da derivada segunda. Sabendo que se:
Nossa curva terá concavidade para baixo.
E se
E nossa curva terá concavidade para cima.
E finalmente, no item (d) vamos usar as informações das partes (a)-(c) para esboçar o gráfico de .
Agora que já sabemos o que fazer em cada item, vem comigo que te mostro como vai ficar tudo isso.
Passo 2
Item a:
Uma função é crescente quando sua derivada é positiva e decrescente quando sua derivada é negativa. Portanto, para avaliar os intervalos onde é crescente ou decrescente, vamos obter a derivada e analisar o seu sinal.
Sendo
Como é uma função composta, usamos a regra da cadeia pra calcular sua derivada. Assim, fazemos
Onde
Aplicando a regra a derivada será:
Como é sempre maior que zero e se e se , então:
é decrescente para valores de no intervalo e crescente no intervalo .
Passo 3
Item b:
Os pontos onde a derivada é zero, pontos críticos são:
Fazendo:
O que só é verdade se:
Como decresce até e cresce a partir dele, é ponto de mínimo local.
Passo 4
Item c:
A concavidade de uma função é indicada pelo sinal da derivada segunda. Quando a derivada segunda é positiva, a função possui concavidade voltada para cima e quando a derivada segunda é negativa, a função possui concavidade voltada para baixo. Então devemos obter a derivada segunda e estudar o seu sinal.
Como a primeira derivada é:
A segunda será calculada usando a regra do quociente, já que essa função é formada pela divisão de outras duas funções.
Assim,
E
Onde
Com
E
Com
E nossa derivada será:
Assim, para
Para
Para
ou
Logo, possui concavidade para cima para valores de nos intervalos e e concavidade para baixo para valores de no intervalo e . E os pontos de inflexão são e .
Passo 5
Item d:
Com as informações obtidas, temos o gráfico:
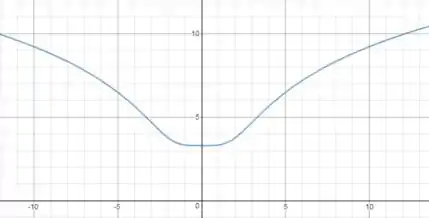
E prontinho.
Resposta
(a) é decrescente para valores de no intervalo e crescente no intervalo .
(b) é ponto de mínimo local.
(c) possui concavidade para cima para valores de nos intervalos e e concavidade para baixo para valores de no intervalo e . E os pontos de inflexão são e .
(d)
