Encontre o volume do sólido que resulta quando a região delimitada por , e gira em torno da reta .
Passo 1
Bom galera, nosso volume é dado pela rotação da região sombreada:
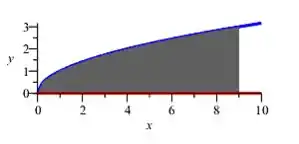
Logo, nossa região é:
Passo 2
Belezinha, a nossa integral para o volume é:
Passo 3
Por fim, resolvemos a integral: