Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.2 - Ex. 35

Encontre (d y)/(d x) usando derivação logarítmica:

y = x root(3)(1 + x^2)

Passo 1

Nem sempre a solução da diferenciação de uma derivada é trivial, mas, se aplicarmos o logaritmo natural em ambos os lados e usarmos suas propriedades, podemos derivar uma função complexa utilizando as propriedades de logaritmo.

Vamos analisar a função dada:

y = x root(3)(1 + x^2)

Agora, aplicando logaritmo na função:

l n ( y ) = l n ( x root(3)(1 + x^2 ))

Com ela, podemos usar as seguintes propriedades de logaritmo:

ln (y) = ln (x) + l n (root(3)(1 + x^2))

ln (y) = ln (x) + (1)/(3) l n (1 + x^2)

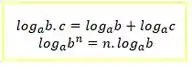
Agora, podemos diferenciar dos dois lados. Isso significa que iremos derivar todos os termos antes e depois da igualdade!!!

Passo 2

Aqui, aplicaremos a derivada em cada termo da igualdade.

ln (y) = ln (x) + (1)/(3) l n (1 + x^2)

(d (ln (y)))/(d x) = (d)/(d x) [ln (x) + (1)/(3) l n (1 + x^2)]

Derivando temos:

(1)/(y) . (d y)/(d x) = (1)/(x) + (2 x)/(3 ( 1 + x^2 ))

Para eliminar o termo (1)/(y) que aparece na diferenciação, multiplicamos ambos os lados pela função y :

(d y)/(d x) = ((1)/(x) + (2 x)/(3 (1 + x^2))) . [ x root(3)(1 + x^2) ]

Resposta

(d y)/(d x) = ((1)/(x) + (2 x)/(3 (1 + x^2))) . [ x root(3)(1 + x^2) ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de Newton para encontrar todas as raízes da equação com precisão de seis casas decimais. e x = 3 - 2 x
Use o método de Newton para encontrar todas as raízes da equação com precisão de seis casas decimais. x - 2 2 = ln ⁡ x
Explique por que a função logarítmica natural y = ln ⁡ x é usada mais vezes no cálculo do que as outras funções logarítmicas y = log a ⁡ x .
Mostre que a função densidade de probabilidade de uma variável aleatória com a distribuição normal tem pontos de inflexão em x = μ ± σ .
Calcule g^' (x) g (x) = log_5 x v