Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 26
Esboce a área da região que está dentro da primeira curva e fora da segunda curva.
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
O problema pede para acharmos a área da região dentro da curva:
e fora da curva
Um esboço das duas curvas é dado a seguir:
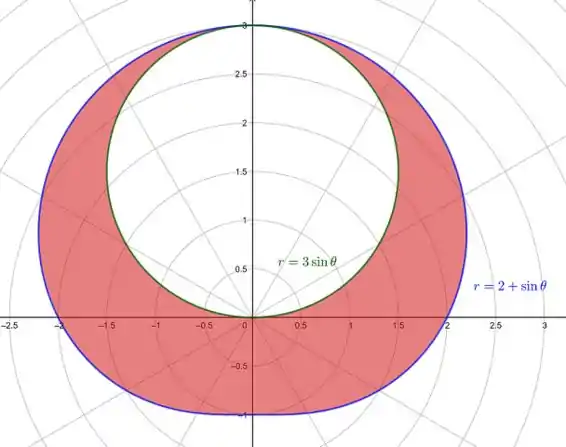
A área sombreada em vermelho é o que devemos encontrar. Subtrairemos a área que é da segunda curva da área da primeira curva.
A área de uma curva parametrizada em coordenadas polares é dada por:
Passo 2
Note que a curva interna é o círculo de raio .
Se não conseguir notar, é só lembrar que:
E
Então a gente tem que:
Então:
Se utilizarmos:
Teremos então que:
Agora podemos substituir:
Completando o quadrado:
Teremos então a equação do círculo de raio .
Passo 3
Assim, basta fazer a área da curva externa e subtrair a área do círculo:
Para a área da curva externa, fazemos:
Veja que o limite de integração será de a , pois o nosso ângulo precisa dar uma volta completa para ‘varrer’ toda a figura e calcular sua área total:
Aí temos que lembrar que:
Portanto,
Vamos então dividir essa integral em várias integrais:
Podemos resolver as duas primeiras, e iremos agora integrar as duas últimas:
Realizando os cálculos:
Temos então:
Portanto, a área pedida é