Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 29
Esboce a área da região que está dentro de ambas as curvas.
Passo 1
O problema pede para acharmos a área da região dentro das curvas
e
Um esboço das duas curvas é dado a seguir:
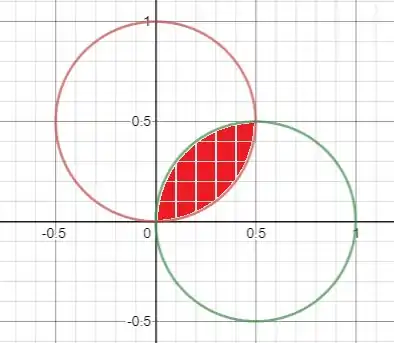
O encontro delas se dá em , que encontramos ao igualarmos ambas as equações.
Note que se dividirmos a região na metade obtemos duas áreas idênticas.
Uma que vai ser a integral da curva vermelha entre e e a outra que será a integral da curva verde entre e .
Vamos fazer só a primeira integral e depois multiplicá-la por .
A área de uma região em coordenadas polares é dada por:
E e é o nosso intervalo de integração.
Passo 2
Vamos fazer só a primeira integral e depois multiplicá-la por :
Vamos usar a fórmula:
Assim,
Portanto,
Logo,
Resposta
Exercícios de Livros Relacionados
Encontre as áreas das regiões nos Exercícios 9-18Dividida pelas cardioides r = 2 ( 1 + cos θ ) e r = 2 ( 1 - cos θ ) .
Encontre os comprimentos das curvas nos exercícios 21-28.A espiral r = θ 2 ,0 ≤ θ ≤ 5 .
Encontre as áreas das regiões nos Exercícios 9-18Dividida pelo círculo r = 2 e pela cardioide r = 2 ( 1 - cos θ ) .
Encontre as áreas das regiões nos Exercícios 1-8Dentro de uma folha da rosa de três pétalas r = cos 3 θ .
Encontre os comprimentos das curvas nos exercícios 21-28.A cardioide r = 1 + cos θ .